Bài tập 5 trang 35 SGK Hình học 11

Bài tập 5 trang 35 SGK Hình học 11

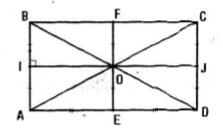
Xét phép đối xứng trục \({D_{{\rm{IJ}}}}\) vì ABCD là hình chữ nhật nên \({\rm{IJ}} \bot AB\) và IA = IB (I là trung điểm của AB, J là trung điểm CD)

Do đó \({D_{{\rm{IJ}}}}(A) = B\)

Tương tự: \({D_{{\rm{IJ}}}}{\rm{(E}}) = F\)

Vì O thuộc IJ nên \({D_{{\rm{IJ}}}}{\rm{(O}}) = O\)

Xét phép vị tự \({V_{(B;2)}},\) ta có \({V_{(B;2)}}(B) = B\)

Vì F và O lần lượt là trung điểm của BC và BD nên \({V_{(B;2)}}(F) = C,{V_{(B;2)}}(O) = D\)

Vậy tam giác BCD là ảnh của tam giác AEO qua phép đồng dạng trên.

-- Mod Toán 11