Bài tập 1 trang 33 SGK Hình học 11

Bài tập 1 trang 33 SGK Hình học 11

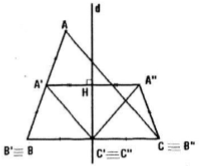
Gọi tam giác A'B'C' là ảnh của tam giác ABC qua \(V_ {\left ( B, \frac{1}{2} \right )}\), khi đó \(V_ {\left ( B, \frac{1}{2} \right )} \ (B)=B\) hay B' trùng với B.

\(A'=V_ {\left ( B, \frac{1}{2} \right )} \ (A)\Leftrightarrow \overrightarrow{BA'}=\frac{1}{2}\overrightarrow{BA}\) hay A' là trung điểm của BA.

\(C'=V_ {\left ( B, \frac{1}{2} \right )} \ (C)\Leftrightarrow \overrightarrow{BC'}=\frac{1}{2}\overrightarrow{BC}\) hay C' là trung điểm của BC. Gọi tam giác A''B''C'' là ảnh của tam giác A'B'C' qua phép đối xứng qua đường trung trực d của BC, khi đó

Đd (B') = C hay B'' trùng với C.

Đd(C') = C' hay C'' trùng với C'.

Gọi H là hình chiếu vuông góc của A' trên d. A' là điểm thoả mãn điều kiện \(\Leftrightarrow \overrightarrow{HA''}=-\overrightarrow{HA'}\) hay H là trung điểm của A'A''.

Vậy tam giác A''B''C'' vừa dựng trên là ảnh của tam giác ABC.

-- Mod Toán 11