Bài tập 1 trang 19 SGK Hình học 11

Bài tập 1 trang 19 SGK Hình học 11

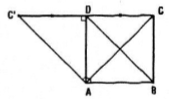
Câu a:

Gọi C'= Đ_o (C) khi đó \(\Delta ACC'\) cân tại A và \(\widehat{ACD}=\widehat{AC'D}=45^0\)

Suy ra \(\widehat{CAC'}=90^0 \ hay \ (OC; \ OC')=90^0\)

Khi đó \(\left\{\begin{matrix} (AC,AC')=90^0\\ AC=AC' \end{matrix}\right. \ hay \ C'=Q_{(A.90^0)}(C)\)

Câu b:

Ta có: \(\left\{\begin{matrix} (AB;AD)=90^0\\ AB=AD \end{matrix}\right.\)

nên \(D=Q_{(A,90^0)} .(B)\)

Vậy ảnh của đường thẳng BC qua phép quay \(Q_{(A,90^0)}\) đường thẳng đi qua C' và D hay chính là đường thẳng CD.

-- Mod Toán 11