Bài tập 7 trang 34 SGK Hình học 11 NC
Bài tập 7 trang 34 SGK Hình học 11 NC
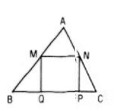
a. Cho tam giác ABC và hình vuông MNPQ như hình 27. Gọi V là phép vị tự tâm A tỉ số \(k = \frac{{AB}}{{AM}}\) . Hãy dựng ảnh của hình vuông MNPQ qua phép vị tự V
b. Từ bài toán ở câu a) hãy suy ra cách giải bài toán sau: Cho tamn giác nhọn ABC, hãy dựng hình vuông MNPQ sao cho hai đỉnh P, Q nằm trên cạnh BC và hai đỉnh M, N lần lượt nằm trên hai cạnh AB và AC
a) Ta có \(\overrightarrow {AB} = k\overrightarrow {AM} ;\overrightarrow {AC} = k\overrightarrow {AN} \) nên phép vị tự V biến điểm M thành điểm B, biến điểm N thành điểm C
Vậy V biến hình vuông MNPQ thành hình vuông BCP’Q’ như trên hình bên
b) Dựng hình vuông BCP’Q’ nằm ngoài tam giác ABC như hình
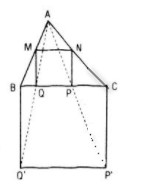
Lấy giao điểm P, Q của BC với các đoạn thẳng tương ứng AP’ và AQ’
Từ P và Q, kẻ các đường thẳng vuông góc với BC, lần lượt cắt AC và AB tại N và M
Khi đó MNPQ chính là hình vuông cần dựng.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
