Bài tập 2 trang 33 SGK Hình học 11

Bài tập 2 trang 33 SGK Hình học 11

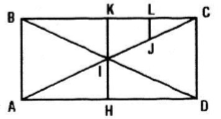
Xét \(\Delta CKI\) ta có LJ là đường trung bình nên \(LJ=\frac{1}{2}KI=\frac{1}{2}IH\)

Do đó \(LJ=\frac{1}{2}IH (1)\)

Xét \(\Delta BCD\) ta có KI là đường trung bình nên \(KI=\frac{1}{2}DC \ (2)\)

và \(KL=\frac{1}{2}KC=\frac{1}{2}HD \ (3)\) 

\(\(IJ=\frac{1}{2} IC \ \ (4)\)

Từ (1), (2), (3), (4) ta có: Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng tỉ số \(\frac{1}{2}\). Vậy hai hình thang JLKI và hình thang IHDC là đồng dạng với nhau.

-- Mod Toán 11