Bài tập 2 trang 19 SGK Hình học 11

Bài tập 2 trang 19 SGK Hình học 11

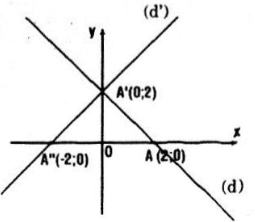
Ta có điểm A'(0;2) là ảnh của điểm A(2;0) qua \(Q_{(O,90^0)}\). Thật vậy:

\(\left\{\begin{matrix} \widehat{AOA}=90^0\\ OA=OA' \end{matrix}\right.\)

Gọi d' là ảnh của d qua \(Q_{(O,90^0)}\) ta có A thuộc d nên A' thuộc d'. Mặt khác \(d'=Q_{(O,90^0)}\) nên \(d'\perp d\) hay vecto chỉ phương \(\vec{u}=(-1;1)\) của d là vecto pháp tuyến của d' vậy d':

\(-1(x-0)+1(y-2)=0\Leftrightarrow x-y+2=0\).

-- Mod Toán 11