Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 1: Phép Dời Hình Và Phép Đồng Dạng Trong Mặt Phẳng
Bài tập 7 trang 35 SGK Hình học 11
Bài tập 7 trang 35 SGK Hình học 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 7 trang 35 SGK Hình học 11
Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O), dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.
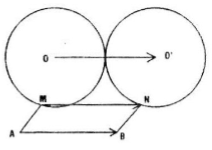
Tứ giác MABN là hình bình hành khi và chỉ khi \(\overrightarrow {MN} = \overrightarrow {AB} \)
Vậy N là ảnh của điểm M qua \({T_\overrightarrow {AB}}\)
Vì \(M \in (O)\) nên \(N \in (O')\) là ảnh của đường tròn (O) qua \({T_\overrightarrow {AB}}\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247
