Bài tập 6 trang 34 SGK Hình học 11

Bài tập 6 trang 34 SGK Hình học 11

Cho hai đường tròn (I; R) và (I’; R’). Khi đó ta có các trường hợp sau:

 * Trường hợp 1: I trùng với I’

Khi đó phép vị tự \({V_{\left( {I,\frac{{R'}}{R}} \right)}}\) và \({V_{\left( {I, - \frac{{R'}}{R}} \right)}}\)biến đường tròn (I; R) thành đường tròn (I’; R’). Thật vậy, gọi M là điểm thuộc (I; R) và \(M' = {V_{\left( {I,\frac{{R'}}{R}} \right)}}(M).\)

\( \Leftrightarrow \overrightarrow {IM'}  = \frac{{R'}}{R}.\overrightarrow {IM} \) hay M’ là giao điểm của tia IM với (I; R) do đó M’ thuộc (I’; R’). Vậy (I’; R’) là ảnh của (I; R) qua \({V_{\left( {I,\frac{{R'}}{R}} \right)}}\). Tương tự cho phép vị tự \({V_{\left( {I,\frac{{R'}}{R}} \right)}}\)

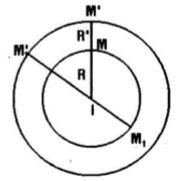
Vậy I là tâm vị tự của hai đường tròn trên.

* Trường hợp 2: I khác I’ và \(R \ne R'\)

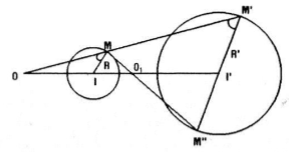
Lấy điểm M bất kỳ thuộc đường tròn (I; R) đường thẳng qua I’ song song với IM cắt đường tròn (I’; R’) tại M’, M’’. Giả sử MM’ cắt II’ tại điểm O, MM’’ cắt II’ tại \({O_1}\) (trong đoạn \(I{I_1}\))

Xét phép vị tự \({V_{\left( {O;\frac{{R'}}{R}} \right)}}\) ta có \({V_{\left( {O;\frac{{R'}}{R}} \right)}}(M) = M'\)

Hay (I’; R’) là ảnh của (I; R) qua \({V_{\left( {O;\frac{{R'}}{R}} \right)}}\)

Vậy O là tâm vị tự của (I; R) và (I’; R’)

Tương tự ta có: (I’; R’) cùng là ảnh của (I; R) qua \({V_{\left( {O;\frac{{R'}}{R}} \right)}}\)

Vậy \({O_1}\) là tâm vị tự của (I; R) và (I’; R’)

Ta gọi O là tâm vị tự ngoài, \({O_1}\)là tâm vị tự trong của hai đường tròn trên.

* Trường hợp 3: I khác I’ và R = R’

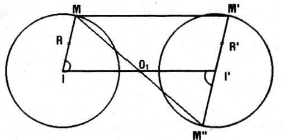
Khi đó MM’ // II’, gọi \({O_1}\)là giao điểm của MM’ và II’

Xét \({V_{\left( {{O_1};\frac{{R'}}{R}} \right)}}\)ta có \({V_{\left( {{O_1};\frac{{R'}}{R}} \right)}}\) (M) = M’’ thuộc (I’; R’) hay (I’; R’) là ảnh của (I; R) qua \({V_{\left( {{O_1};\frac{{R'}}{R}} \right)}}\)

Vậy \({O_1}\)là tâm vị tự của (I; R) và (I’; R’).

-- Mod Toán 11