Đề trắc nghiệm ôn thi học kì 1 môn Toán lớp 12 năm 2018 - 2019 có lời giải -...
Câu 1 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Cạnh bên SA vuông góc với mặt phẳng (ABCD) và \(SC = \sqrt 5 \). Tính thể tích khối chóp S.ABCD
A. \(V = \frac{{\sqrt 3 }}{3}\)
B. \(V = \frac{{\sqrt 3 }}{6}\)
C. \(V = \sqrt 3 \)
D. \(V = \frac{{\sqrt 15 }}{3}\)
Câu 2 : Diện tích xung quanh của hình nón tròn xoay ngoại tiếp tứ diện đều cạnh \(a\) là:
A. \({S_{xq}} = \frac{{\pi {a^2}}}{3}\)
B. \({S_{xq}} = \frac{{2\pi {a^2}}}{3}\)
C. \({S_{xq}} = \frac{{\pi \sqrt 3 {a^2}}}{3}\)
D. \({S_{xq}} = \frac{{2\pi \sqrt 3 {a^2}}}{3}\)
Câu 3 : Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\) có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng \(\Delta :y = 3x + 1\) có phương trình là:
A. \(y = 3x - 1\)
B. \(y = 3x - \frac{{26}}{3}\)
C. \(y = 3x - 2\)
D. \(y = 3x - \frac{{29}}{3}\)
Câu 4 : Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{\sqrt {{x^2} + 1} }}\) , giá trị lớn nhất của hàm số \(f(x)\) trên tập xác định của nó là:
A. \(2\)
B. \(4\)
C. \(2\sqrt 2 .\)
D. \(\sqrt {10} .\)
Câu 5 : Tìm các giá trị của tham số \(m\) để hàm số : \(y = \frac{1}{3}{x^3} + m{x^2} + \left( {m + 6} \right)x - \left( {2m + 1} \right)\) luôn đồng biến trên R:
A. \(m \le - 2\)
B. \(m \ge 3\)
C. \( - 2 \le m \le 3\)
D. \(m \le - 2\) hoặc \(m \ge 3\)
Câu 6 : Gọi giá trị cực đại và giá trị cực tiểu của hàm số \(y = {x^3} - 3x + 2\) lần lượt là \({y_{CD}},{y_{CT}}\). Tính \(3{y_{CD}} - 2{y_{CT}}\) ?
A. \(3{y_{CD}} - 2{y_{CT}} = - 12\)
B. \(3{y_{CD}} - 2{y_{CT}} = - 3\)
C. \(3{y_{CD}} - 2{y_{CT}} = 3\)
D. \(3{y_{CD}} - 2{y_{CT}} = 12\)
Câu 7 : Đồ thị hàm số \(y = \frac{{x + 2017}}{{\sqrt {{x^2} - 5} }}\) có số đường tiệm cận là:
A. 1
B. 2
C. 3
D. 4
Câu 8 : Bất phương trình \(3{\log _3}(x - 1) + {\log _{\sqrt[3]{3}}}(2x - 1) \le 3\) có tập nghiệm là :
A. \(\left( {1;2} \right]\)
B. \(\left[ {1;2} \right]\)
C. \(\left[ {\frac{{ - 1}}{2};2} \right]\)
D. \(\left( {\frac{{ - 1}}{2};2} \right]\)
Câu 9 : Tổng bình phương các nghiệm của phương trình \({5^{3x - 2}} = {\left( {\frac{1}{5}} \right)^{ - {x^2}}}\) bằng:
A. 0
B. 5
C. 2
D. 3
Câu 10 : Nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\frac{{{x^2} - 3x + 2}}{x} > 0\) là:
A.
\(\left[ \begin{array}{l}
x < 0\\
2 - \sqrt 2 < x < 2 + \sqrt 2
\end{array} \right.\)
B.
\(\left[ \begin{array}{l}
2 - \sqrt 2 \le x < 1\\
2 < x \le 2 + \sqrt 2
\end{array} \right.\)
C.
\(\left[ \begin{array}{l}
2 - \sqrt 2 < x < 1\\
2 < x \le 2 + \sqrt 2
\end{array} \right.\)
D.
\(\left[ \begin{array}{l}
x < 0\\
x > 2 - \sqrt 2
\end{array} \right.\)
Câu 11 : Tập nghiệm của bất phương trình \({4^x} - {2^x} - 2 < 0\) là:
A. \(\left( {1; + \infty } \right)\)
B. \(\left( { - \infty ;1} \right)\)
C. \(\left( {2; + \infty } \right)\)
D. \(\left( { - \infty ;2} \right)\)
Câu 12 : Cho hàm số \(f\left( x \right) = \log \left[ {100\left( {x - 3} \right)} \right]\). Khẳng định nào sau đây sai ?
A. Tập xác định của hàm số \(f(x)\) là \(D = \left[ {3; + \infty } \right)\).
B. \(f\left( x \right) + 2\log \left( {x - 3} \right)\) với \(x>3\)
C. Đồ thị hàm số \(f(x)\) đi qua điểm \((4;2)\).
D. Hàm số \(f(x)\) đồng biến trên \(\left( {3; + \infty } \right)\).
Câu 13 : Tìm tất cả các giá trị của \(m\) để hàm số \(y = {\log _3}\left( {{x^2} - 5x + m} \right)\) xác định trên R.
A. \(m > \frac{{25}}{4}\)
B. \(m \ge 0\)
C. \(m>0\)
D. \(m \ge \frac{{25}}{4}\)
Câu 14 : Cho hình chóp S.ABC có đáy là tam giác đều cạnh \(a\) cạnh bên SA vuông góc với đáy và thể tích của khối chóp đó bằng \(\frac{{{a^3}}}{4}.\) Tính cạnh bên SA.
A. \(\frac{{a\sqrt 3 }}{2}.\)
B. \(2a\sqrt 3 .\)
C. \(a\sqrt 3 .\)
D. \(\frac{{a\sqrt 3 }}{3}.\)
Câu 15 : Cho hình chóp S.ABCDcó đáy ABCD là hình thoi cạnh \(a\) \(SA \bot \left( {ABCD} \right).\) Gọi M là trung điểm BC. Biết \(\widehat {DAB} = {120^o},\widehat {SMA} = {45^o}.\) Khoảng cách từ D đến mặt phẳng (SBC) bằng:
A. \(\frac{{a\sqrt 6 }}{6}\)
B. \(\frac{{a\sqrt 6 }}{3}\)
C. \(\frac{{a\sqrt 6 }}{5}\)
D. \(\frac{{a\sqrt 6 }}{4}\)
Câu 16 : Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng \(a\). Diện tích xung quanh của hình nón bằng:
A. \(\frac{{\pi {a^2}}}{2}\)
B. \(\frac{{\pi {a^2}\sqrt 2 }}{2}\)
C. \(\frac{{3\pi {a^2}}}{2}\)
D. \(\pi {a^2}\)
Câu 17 :
Một cái phễu rỗng phần trên có kích thước như hình vẽ. Diện tích xung quanh của phễu là:.png)
A. \({S_{xq}} = 360\pi \,\,{\rm{c}}{{\rm{m}}^2}\)
B. \({S_{xq}} = 424\pi \,\,{\rm{c}}{{\rm{m}}^2}\)
C. \({S_{xq}} = 296\pi \,\,{\rm{c}}{{\rm{m}}^2}\)
D. \({S_{xq}} = 960\pi \,\,{\rm{c}}{{\rm{m}}^2}\)
Câu 18 : Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh \(a\) \(\widehat {BCD} = {120^0}\) và \(AA' = \frac{{7a}}{2}\). Hình chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A'B'C'D'.
A. \(V = 12{a^3}\)
B. \(V = 3{a^3}\)
C. \(V = 9{a^3}\)
D. \(V = 6{a^3}\)
Câu 19 : Khối lăng trụ ABC.A'B'C' có thể tích bằng \(a^3\), đáy là tam giác đều cạnh bằng \(2a\). Tính khoảng cách giữa AB và B'C'.
A. \(\frac{{4a}}{{\sqrt 3 }}\)
B. \(\frac{a}{{\sqrt 3 }}\)
C. \(a\)
D. \(a\sqrt 3 \)
Câu 20 : Tìm tập hợp tất cả các giá trị của tham số thực \(m\) để hàm số \(y = \ln \left( {{x^2} + 4} \right) - mx + 3\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
A. \(\left( { - \infty ; - \frac{1}{2}} \right]\)
B. \(\left( { - \infty ; - \frac{1}{2}} \right)\)
C. \(\left[ { - \frac{1}{2};\frac{1}{2}} \right]\)
D. \(\left[ {\frac{1}{2}; + \infty } \right)\)
Câu 21 : Cho các số thực \(1 > a > b > 0\). Tìm giá trị nhỏ nhất của biểu thức \(P = - 3{\log _{{a^4}}}\frac{a}{b} + \log _b^2\left( {ab} \right)\)
A. \({P_{\min }} = 3\)
B. \({P_{\min }} = 4\)
C. \({P_{\min }} = \frac{5}{2}\)
D. \({P_{\min }} = \frac{3}{2}\)
Câu 22 :
Một cái tục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là 5 cm, chiều dài lăn là 23 cm (hình dưới). Sau khi lăn trọn 15 vòng thì trục lăn tạo trên sân phẳng một diện diện tích là.PNG)
A. \(1725\pi {\rm{c}}{{\rm{m}}^3}.\)
B. \(3450\pi {\rm{c}}{{\rm{m}}^2}.\)
C. \(1725\pi {\rm{c}}{{\rm{m}}^2}.\)
D. \(862,5\pi {\rm{c}}{{\rm{m}}^2}.\)
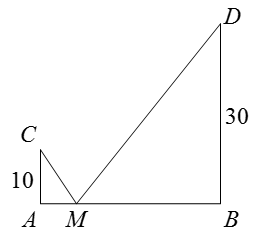
Câu 23 :
Người ta cắt miếng bìa hình tam giác cạnh bằng 10 cm như hình bên và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích của khối tứ diện tạo thành..png)
A. \(V = \frac{{250\sqrt 2 }}{{12}}{\rm{c}}{{\rm{m}}^3}.\)
B. \(V = 250\sqrt 2 {\rm{c}}{{\rm{m}}^3}.\)
C. \(V = \frac{{125\sqrt 2 }}{{12}}{\rm{c}}{{\rm{m}}^3}.\)
D. \(V = \frac{{1000\sqrt 2 }}{3}{\rm{c}}{{\rm{m}}^3}.\)
Câu 24 : Tìm tất cả các giá trị thực của tham số \(m\) sao cho đường thẳng \(y=m\) cắt đồ thị hàm số \(y = {x^3} - 3x + 1\) tại ba điểm phân biệt, trong đó có đúng hai điểm phân biệt có hoành độ dương?
A. \( - 1 < m < 3.\)
B. \( 1 < m < 3.\)
C. \( - 1 < m < 1.\)
D. \(m=1\)
Câu 26 : Tất cả các giá trị của \(m\) để bất phương trình \((3m + 1){.12^x} + (2 - m){.6^x} + {3^x} < 0\) có nghiệm đúng \(\forall x > 0\) là:
A. \(\left( { - 2; + \infty } \right)\)
B. \(( - \infty ; - 2]\)
C. \(\left( { - \infty ; - \frac{1}{3}} \right)\)
D. \(\left( { - 2; - \frac{1}{3}} \right)\)
Câu 27 : Cho phương trình \({4.5^{\log (100{x^2})}} + {25.4^{\log (10x)}} = {29.10^{1 + \log x}}\). Gọi \(a\) và \(b\) lần lượt là 2 nghiệm của phương trình. Khi đó giá trị biểu thức \(ab + 2017\) bằng:
A. \(2017\)
B. \(10\)
C. \(2018\)
D. \(\frac{1}{{10}}\)
Câu 28 :
Cho hàm số \(y = \frac{{\left( {m - 1} \right){x^3}}}{3} + \left( {m - 1} \right){x^2} + 4x - 1\). Hàm số đã cho đạt cực tiểu tại \(x_1\) , đạt cực đại tại \(x_2\) đồng thời \(x_1 \)>
A. \(m>5\)
B. \(m=1\) hoặc \(m=5\)
C. \(m<1\) hoặc \(m>5\)
D. \(m<1\)
Câu 29 : Hàm số \(y = \frac{{x - {m^2}}}{{x + 1}}\) có giá trị nhỏ nhất trên đoạn \(\left[ {0;1} \right]\) bằng \(-1\) khi:
A.
\(\left[ \begin{array}{l}
m = 1\\
m = - 1
\end{array} \right.\)
B.
\(\left[ \begin{array}{l}
m = \sqrt 3 \\
m = - \sqrt 3
\end{array} \right.\)
C. \(m=-2\)
D. \(m=3\)
Câu 30 : Cho khối trụ (T) có thiết diện qua trục là một hình vuông có diện tích bằng 4. Tính diện tích xung quanh Sxq của khối trụ (T).
A. \({S_{xq}} = 4\pi \)
B. \({S_{xq}} = 2\pi \)
C. \({S_{xq}} = 8\pi \)
D. \({S_{xq}} = 4\sqrt 2 \)
Câu 31 : Khi sản xuất vỏ lon sữa Ông Thọ hình trụ, các nhà sản xuất luôn đặt chỉ tiêu sao cho chi phí sản xuất vỏ lon là nhỏ nhất, tức là nguyên liệu ( sắt tây) được dùng là ít nhất. Hỏi khi đó diện tích toàn phần \(S_{tp}\) của lon sữa là bao nhiêu, khi nhà sản xuất muốn thể tích của hộp là \(V cm^3\).
A. \({S_{tp}} = 3\sqrt[3]{{\frac{{\pi {V^2}}}{4}}}\)
B. \({S_{tp}} = 6\sqrt[3]{{\frac{{\pi {V^2}}}{4}}}\)
C. \({S_{tp}} = 3\sqrt {\frac{{\pi {V^2}}}{4}} \)
D. \({S_{tp}} = 6\sqrt {\frac{{\pi {V^2}}}{4}} \)
Câu 32 : Một hình trụ (T) có hai đáy là hai hình tròn nội tiếp hình vuông cạnh \(a\). Tính thể tích \(V_{(T)}\) của khối trụ đó, biết chiều cao của khối trụ bằng \(h=a\)?
A. \({V_{\left( T \right)}} = \frac{1}{2}{a^3}\pi \)
B. \({V_{\left( T \right)}} = \frac{1}{4}{a^3}\pi \)
C. \({V_{\left( T \right)}} = \frac{1}{3}{a^3}\pi \)
D. \({V_{\left( T \right)}} ={a^3}\pi \)
Câu 33 : Tìm tất cả các giá trị \(m\) để hàm số \(y = \left( {m - 1} \right){x^3} - m{x^2} + 2x + 1\) luôn nghịch biến trên R?
A. \(3 - \sqrt 3 < m < 1\)
B. \(1 < m < 3 + \sqrt 3 \)
C. \(\forall x \in R\)
D. \(3 - \sqrt 3 < m < 3 + \sqrt 3 \)
Câu 34 : Với tất cả giá trị nào của \(m\) thì hàm số \(y = m{x^4} + \left( {m - 1} \right){x^2} + 1 - 2m\) chỉ có một cực trị?
A. \(m \ge 1\)
B. \(m \le 0\)
C. \(0 \le m \le 1\)
D. \(m \le 0 \vee m \ge 1\)
Câu 35 : Cho hàm số \(y = {x^4} - 2m{x^2} + 1 - m\). Tìm tất cả các giá trị thực của \(m\) để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ O làm trực tâm.
A. \(m=1\)
B. \(m=2\)
C. \(m=0\)
D. \(m=-1\)
Câu 36 : Tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 6\) trên \([-4;4]\).
A. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} f\left( x \right) = 21\)
B. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} f\left( x \right) = -14\)
C. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} f\left( x \right) = 11\)
D. \(\mathop {Min}\limits_{\left[ { - 4;4} \right]} f\left( x \right) = -7\)
Câu 37 : Một xe buýt của hãng xe A có sức chứa tối đa là 50 hành khách. Nếu một chuyến xe buýt chở \(x\) hành khách thì giá tiền cho mỗi hành khách là: \(20{\left( {3 - \frac{x}{{40}}} \right)^2}\) (nghìn đồng). Khẳng định nào dưới đây là đúng?
A. Một chuyến xe buýt thu được số tiền nhiều nhất bằng 3.200.000 đồng.
B. Một chuyến xe buýt thu được số tiền nhiều nhất khi có 45 hành khách.
C. Một chuyến xe buýt thu được số tiền nhiều nhất bằng 2.700.000 đồng.
D. Một chuyến xe buýt thu được số tiền nhiều nhất khi có 50 hành khách.
Câu 38 : Tìm số tiệm cận của đồ thị hàm số \(y = \frac{{x + 1}}{{\sqrt {{x^2} - 1} }}\).
A. 2
B. 3
C. 4
D. 0
Câu 39 : Viết phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right) = \frac{2}{3}{x^3} - {x^2} + 1\) tại điểm có hoành độ \(x_0\) là nghiệm của phương trình\(f''(x_0)=10\).
A. \(y=12x-23\)
B. \(y=12x-24\)
C. \(y=12x-25\)
D. \(y=12x-26\)
Câu 40 : Đồ thị của hàm số \(y = - {x^3} + 3{x^2} + 2x - 1\) và đồ thị của hàm số \(y = {x^2} - 2x - 1\) có tất cả bao nhiêu điểm chung?
A. 2
B. 0
C. 1
D. 3
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247