Giải tích 12 - Phần giải tích !!
Câu 12 : Chứng minh rằng hàm số đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Câu 14 : Chứng minh các bất đẳng thức sau:
Câu 15 : Chứng minh các bất đẳng thức sau:
Câu 16 : Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
Câu 17 : Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
Câu 21 : Chứng minh hàm số y = |x| không có đạo hàm tại x = 0. Hàm số có đạt cực trị tại điểm đó không ?
Câu 31 : Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Câu 32 : Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn luôn có một cực đại và một điểm cực tiểu.
Câu 37 :
Cho hàm số y = 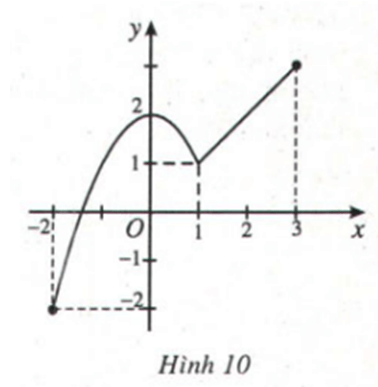
Câu 38 : Lập bảng biến thiên của hàm số .
Câu 43 : Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Câu 44 : Trong tất cả các hình chữ nhật có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Câu 47 : Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Câu 48 : Trong tất cả các hình chữ nhật có diện tích , hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Câu 55 : Tìm các tiệm cận của đồ thị hàm số:
Câu 56 : Tìm các tiệm cận của đồ thị hàm số:
Câu 57 : Tìm các tiệm cận của đồ thị hàm số:
Câu 58 : Tìm các tiệm cận của đồ thị hàm số:
Câu 64 : Cho hàm số
Câu 65 : Cho hàm số
Câu 66 : Cho hàm số
Câu 67 : Cho hàm số
Câu 68 : Cho hàm số
Câu 69 : Cho hàm số
Câu 70 : Cho hàm số:
Câu 71 : Cho hàm số:
Câu 76 : Phát biểu các điều kiện đồng biến và nghịch biến của hàm số. Tìm các khoảng đơn điệu của hàm số
Câu 84 : Giải phương trình f'(x - 1) > 0.
Câu 89 : Cho hàm số: (m là tham số).
Câu 90 : Cho hàm số: (m là tham số).
Câu 91 : Cho hàm số: (m là tham số).
Câu 95 : Cho hàm số
Câu 96 : Cho hàm số
Câu 97 : Cho hàm số
Câu 100 : Xác định m sao cho độ dài MN nhỏ nhất.
Câu 102 : Cho hàm số
Câu 103 : Cho hàm số
Câu 104 : Cho hàm số
Câu 105 : Tính
Câu 106 : Dựa vào đồ thị của các hàm số và (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình .
Câu 107 : Chứng minh tính chất
Câu 109 : Rút gọn biểu thức
Câu 110 : So sánh các số
Câu 111 : Tính:
Câu 112 : Tính
Câu 113 : Tính
Câu 114 : Tính
Câu 115 : Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
Câu 116 : Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
Câu 117 : Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
Câu 118 : Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
Câu 119 : Viết các số sau theo thứ tự tăng dần:
Câu 120 : Viết các số sau theo thứ tự tăng dần:
Câu 121 : Rút gọn các biểu thức sau:
Câu 122 : Rút gọn các biểu thức sau:
Câu 123 : Rút gọn các biểu thức sau:
Câu 124 : Rút gọn các biểu thức sau:
Câu 125 : Chứng minh rằng:
Câu 126 : Chứng minh rằng:
Câu 127 : Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng:
Câu 128 : Tính đạo hàm của các hàm số:
Câu 129 : Tính đạo hàm của hàm số
Câu 130 : Tìm tập xác định của các hàm số:
Câu 131 : Tìm tập xác định của các hàm số:
Câu 132 : Tìm tập xác định của các hàm số:
Câu 133 : Tìm tập xác định của các hàm số:
Câu 134 : Tính đạo hàm của các hàm số:
Câu 135 : Tính đạo hàm của các hàm số:
Câu 136 : Tính đạo hàm của các hàm số:
Câu 137 : Tính đạo hàm của các hàm số: y =
Câu 140 : Hãy so sánh các số sau với 1:
Câu 141 : Hãy so sánh các số sau với 1:
Câu 142 : Hãy so sánh các số sau với 1:
Câu 143 : Hãy so sánh các số sau với 1:
Câu 144 : So sánh
Câu 145 : So sánh
Câu 146 : So sánh
Câu 147 : Tìm x để:
Câu 148 : Tìm x để:
Câu 149 : Tìm x để:
Câu 150 : Tìm x để:
Câu 151 : Tính
Câu 152 : Có các số x, y nào để hay không ?
Câu 153 : Hãy chứng minh các tính chất trên
Câu 155 : Cho .
Câu 156 : Tính .
Câu 157 : Cho . Tính và so sánh các kết
Câu 158 : Cho a = 4, b = 64, c = 2. Tính
Câu 159 : Không sử dụng máy tính, hãy tính:
Câu 160 : Không sử dụng máy tính, hãy tính:
Câu 161 : Không sử dụng máy tính, hãy tính:
Câu 162 : Không sử dụng máy tính, hãy tính:
Câu 163 : Tính
Câu 164 : Tính
Câu 165 : Tính
Câu 166 : Tính
Câu 167 : Rút gọn biểu thức:
Câu 168 : Rút gọn biểu thức:
Câu 169 : So sánh các cặp số sau:
Câu 170 : So sánh các cặp số sau:
Câu 171 : So sánh các cặp số sau:
Câu 172 : Cho Hãy tính theo a,b
Câu 173 : Cho . Hãy tính theo c
Câu 176 : Tìm đạo hàm của hàm số
Câu 178 : Vẽ đồ thị của các hàm số:
Câu 179 : Vẽ đồ thị của các hàm số:
Câu 180 : Tính đạo hàm
Câu 181 : Tính đạo hàm
Câu 182 : Tính đạo hàm
Câu 183 : Tìm tập xác định của các hàm số:
Câu 184 : Tìm tập xác định của các hàm số:
Câu 185 : Tìm tập xác định của các hàm số:
Câu 186 : Vẽ đồ thị của các hàm số: y=logx
Câu 187 : Vẽ đồ thị của các hàm số:
Câu 188 : Tính đạo hàm của các hàm số
Câu 189 : Tính đạo hàm của các hàm số
Câu 190 : Tính đạo hàm của các hàm số
Câu 195 : Giải phương trình ( bằng cách đặt ẩn phụ
Câu 196 : Giải phương trình l.
Câu 197 : Giải các phương trình mũ:
Câu 198 : Giải các phương trình mũ:
Câu 199 : Giải các phương trình mũ:
Câu 200 : Giải các phương trình mũ:
Câu 201 : Giải các phương trình mũ:
Câu 202 : Giải các phương trình mũ:
Câu 203 : Giải các phương trình mũ:
Câu 204 : Giải các phương trình mũ:
Câu 205 : Giải các phương trình lôgarit:
Câu 206 : Giải các phương trình lôgarit:
Câu 207 : Giải các phương rình lôgarit:
Câu 208 : Giải các phương rình lôgarit:
Câu 209 : Giải phương trình:
Câu 210 : Giải phương trình:
Câu 211 : Giải phương trình:
Câu 213 : Giải bất phương trình .
Câu 215 : Giải bất phương trình (1)
Câu 216 : Tính
Câu 217 : Tính
Câu 218 : Tính
Câu 219 : Tính
Câu 220 : Giải các bất phương trình:
Câu 221 : Giải các bất phương trình:
Câu 222 : Tính
Câu 223 : Tính
Câu 224 : Tính
Câu 225 : Giải các bất phương trình:
Câu 226 : Giải các bất phương trình:
Câu 227 : Giải các bất phương trình:
Câu 228 : Giải các bất phương trình:
Câu 230 : Hãy nêu các tính chất của hàm lũy thừa
Câu 232 : Tìm tập xác định của hàm số:
Câu 233 : Tìm tập xác định của hàm số:
Câu 234 : Tìm tập xác định của hàm số:
Câu 235 : Tìm tập xác định của hàm số:
Câu 236 : Biết . Hãy tính
Câu 237 : Cho
Câu 238 : Cho
Câu 239 : Giải các phương trình:
Câu 240 : Giải các phương trình:
Câu 241 : Giải các phương trình:
Câu 242 : Giải các phương trình:
Câu 243 : Giải các phương trình:
Câu 244 : Giải các phương trình:
Câu 245 : Giải các bất phương trình:
Câu 246 : Giải các bất phương trình:
Câu 247 : Giải các bất phương trình:
Câu 248 : Giải các bất phương trình:
Câu 252 : Hãy chứng minh Định lý 1.
Câu 253 : Hãy chứng minh Tính chất 3.
Câu 256 : theo t và dt.
Câu 262 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 263 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 264 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 265 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 266 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 267 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 268 : Tìm hiểu nguyên hàm của các hàm số sau:
Câu 274 : Cho tích phân
Câu 277 : Hãy chứng minh các tính chất 1 và 2.
Câu 279 : Từ đó tính
Câu 280 : Tính các tích phân sau:
Câu 281 : Tính các tích phân sau:
Câu 282 : Tính các tích phân sau:
Câu 283 : Tính các tích phân sau:
Câu 284 : Tính các tích phân sau:
Câu 285 : Tính các tích phân sau:
Câu 286 : Tính các tích phân sau:
Câu 287 : Tính các tích phân sau:
Câu 288 : Tính bằng hai phương pháp:
Câu 289 : Tính diện tích hình thang vuông được giới hạn các đường thẳng y = -2x – 1, y = 0, x = 1 và x = 5.
Câu 290 : Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h.
Câu 303 : Tìm nguyên hàm của các hàm số sau:
Câu 304 : Tìm nguyên hàm của các hàm số sau:
Câu 305 : Tìm nguyên hàm của các hàm số sau:
Câu 306 : Tìm nguyên hàm của các hàm số sau:
Câu 307 : Tính:
Câu 308 : Tính:
Câu 309 : Tính:
Câu 310 : Tính:
Câu 311 : Tính:
Câu 312 : Tính:
Câu 313 : Tính:
Câu 314 : Tính:
Câu 315 : Tính:
Câu 316 : Tính:
Câu 322 : Số phức nào có môđun bằng 0 ?
Câu 331 : Tìm các số thực x và y, biết:
Câu 332 : Tìm các số thực x và y, biết:
Câu 333 : Tìm các số thực x và y, biết:
Câu 335 : Tính |z|, với:
Câu 336 : Tính |z|, với:
Câu 337 : Tính |z|, với: z = -5
Câu 338 : Tính |z|, với: z = i căn 3
Câu 339 : Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: |z| = 1
Câu 340 : Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: |z| ≤ 1
Câu 341 : Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: 1<|z| ≤ 2
Câu 342 : Tìm z, biết:
Câu 343 : Tìm z, biết: z = -√2 + i√3
Câu 344 : Tìm z, biết: z = 5
Câu 345 : Tìm z, biết: z = 7i
Câu 353 : Tính α+ β,α- β với: α = 3, β = 2i
Câu 354 : Tính α+ β,α- β với: α = 1 - 2i, β = 6i
Câu 355 : Tính α+ β,α- β với: α = 15; β = 4 - 2i
Câu 358 : Thực hiện các phép tính sau: 5(4 + 3i)
Câu 359 : Thực hiện các phép tính sau: (-2 - 5i)4i
Câu 361 : Tính:
Câu 362 : Tính:
Câu 364 : Thực hiện các phép chia sau:
Câu 365 : Thực hiện các phép chia sau:
Câu 366 : Thực hiện các phép chia sau:
Câu 367 : Thực hiện các phép chia sau:
Câu 368 : Thực hiện các phép chia sau:
Câu 369 : Tìm nghịch đảo của z là: z = 1 + 2i
Câu 370 : Tìm nghịch đảo của z là: z = - 3i
Câu 371 : Tìm nghịch đảo của z là: z = i
Câu 372 : Tìm nghịch đảo của z là: z = 5 +
Câu 374 : Thực hiện các phép tính sau:
Câu 376 : Thực hiện các phép tính sau:
Câu 379 : Giải các phương trình sau:
Câu 381 : Tìm các căn bậc hai phức của các số sau:
Câu 388 : Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và làm nghiệm.
Câu 392 : Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a, b , c?
Câu 399 : Chứng tỏ rằng với mọi số thực z, ta luôn phần thực và phần ảo của nó không vượt quá mô đun của nó.
Câu 401 : Thực hiện các phép tính sau:
Câu 402 : Thực hiện các phép tính sau:
Câu 403 : Thực hiện các phép tính sau:
Câu 420 : Nhắc lại định nghĩa số phức, số phức liên hợp, mô đun của số phức. Biểu diễn hình học của số phức.
Câu 421 : Cho hàm số f(x)=a-2(a+1)x+a+2 (a ≠ 0)
Câu 422 : Cho hàm số f(x)=a-2(a+1)x+a+2 (a ≠ 0)
Câu 423 : Cho hàm số
Câu 424 : Cho hàm số
Câu 425 : Cho hàm số y = + bx+1
Câu 426 : Cho hàm số y = + bx+1
Câu 427 : Cho hàm số y = + bx+1
Câu 430 : Cho hàm số y = + b
Câu 431 : Cho hàm số y = + b
Câu 432 : Cho hàm số y = + b
Câu 433 : Cho hàm số
Câu 434 : Cho hàm số
Câu 435 : Cho hàm số
Câu 436 : Cho hàm số
Câu 437 : Cho hàm số
Câu 442 : Giải các phương trình sau:
Câu 443 : Giải các phương trình sau:
Câu 444 : Giải các phương trình sau:
Câu 445 : Giải các phương trình sau:
Câu 446 : Giải các bất phương trình sau:
Câu 447 : Giải các bất phương trình sau:
Câu 448 : Giải các bất phương trình sau:
Câu 449 : Giải các bất phương trình sau:
Câu 467 : Trên mặt phẳng tọa độ, hãy tìm tập hợp các điểm biểu diễn số phức z thỏa mãn từng bất đẳng thức:
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247

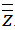 . Nêu nhận xét.
. Nêu nhận xét.