Chương 4: Giới Hạn

Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã). Gọi u_n là khối lượng chất phóng xạ còn sót lại sau chu kì thứ n.

a) Tìm số hạng tổng quát u_n của dãy số \((u_n)\).

b) Chứng minh rằng \((u_n)\) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, cho biết chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \(10^{-6} g\).

Biết dãy số \((u_n )\) thỏa mãn  \(|u_n -1| <\frac{1}{n^{3}}\) với mọi n. Chứng minh rằng lim \(u_n =1\).

Tìm giới hạn sau:

a)  \(lim\frac{6n - 1}{3n +2}\);

b) \(lim\frac{3n^{2}+n-5}{2n^{2}+1}\);

c)  \(lim\frac{3^{n}+5.4^{n}}{4^{n}+2^{n}}\);

d)  \(lim\frac{\sqrt{9n^{2}-n+1}}{4n -2}\).

Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh dấu 1, 2, 3, ..., n trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó.

Giả sử quy trình tô màu của Mickey có thể tiến ra vô hạn.

a) Gọi u_n là diện tích của hình vuông màu xám thứ n. Tính \(u_1 , u_2 , u_3\) và \(u_n\).

b) Tính lim\(S_n\) với \(S_n = u_1 + u_2 + u_3 + ... + u_n\) .

Tính tổng  \(S = -1 + \frac{1}{10}-\frac{1}{10^{2}}+...+ \frac{(-1)^{n}}{10^{n-1}}\) + ...

Cho số thập phân vô hạn tuần hoàn a = 1, 020 020 ... (chu kì là 02). Hãy viết a dưới dạng một phân số.

Tính các giới hạn sau:

a) \(lim (n^3 + 2n^2 - n + 1)\);

b) \(lim (-n^2 + 5n - 2)\);

c) \(lim(\sqrt{n^{2}-n}-n)\) ;

d) (\(lim(\sqrt{n^{2}-n}+n)\).

Cho hai dãy số \((u_n)\)và \((v_n)\). Biết \(lim u_n = 3, lim v_n = +\infty .\)

Tính các giới hạn:

a)  \(lim\frac{3u_{n}-1}{u_{n}+ 1};\)

b)  \(lim\frac{v_{n}+ 2}{v^{2}_{n}-1}\).

Dùng định nghĩa tìm các giới hạn sau:

a) \(\underset{x\rightarrow 4}{lim} \ \frac{x+1}{3x - 2}\);

b) \(\underset{x \rightarrow +\infty }{lim}\frac{2-5x^{2}}{x^{2}+3}\).

Cho hàm số \(f(x) =\left\{\begin{matrix} \sqrt{x}+1; &x\geq 0 \\ 2x;& x <0 \end{matrix}\right.\)

và các dãy số \((u_n)\) với  \(u_n =\frac{1}{n}\), \((v_n)\) với \(v_n = -\frac{1}{n}\).

Tính \(lim u_n, lim v_n, lim f (u_n)\)và \(lim (v_n).\)

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0 ?

Tính các giới hạn sau:

a) \(\underset{x\rightarrow -3}{lim} \frac{x^{2 }-1}{x+1}\);

b) \(\underset{x\rightarrow -2}{lim}\frac{4-x^{2}}{x + 2}\);

c) \(\underset{x\rightarrow 6}{lim} \frac{\sqrt{x + 3}-3}{x-6}\);

d) \(\underset{x\rightarrow +\infty }{lim} \frac{2x-6}{4-x}\);

e) \(\underset{x\rightarrow +\infty }{lim} \frac{17}{x^{2}+1}\);

f) \(\underset{x\rightarrow +\infty }{lim} \frac{-2x^{2}+x -1}{3 +x}\).

Tính các giới hạn sau:

a) \(\underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}}\);

b) \(\underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1}\);

c) \(\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}\).

Cho hàm số  \(f(x) =\frac{x+2}{x^{2}-9}\) có đồ thị như hình dưới đây:

a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x \rightarrow -\infty\)

\(x \rightarrow 3^-\) và \(x \rightarrow 3^+\).

b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

\(\underset{x\rightarrow -\infty }{lim} f(x)\) với f(x) được xét trên khoảng (-3; -3),

\(\underset{x\rightarrow 3^{-}}{lim}f(x)\) với f(x) được xét trên khoảng (-3,3),

\(\underset{x\rightarrow -3^{+}}{lim}f(x)\) với f(x) được xét trên khoảng (-3; 3).

Tính:

a) \(\lim_{+\infty } (x^4 - x^2 + x - 1)\) ;

b) \(\lim_{-\infty } (-2x^3 + 3x^2 -5 )\);

c) \(\lim_{-\infty } \sqrt{x^2-2x+5}\)

d) \(\lim_{+\infty } \frac{\sqrt{x^2+1}+x}{5-2x}\)

Dùng định nghĩa xét tính liên tục của hàm số \(f(x) = x^3 + 2x - 1\) tại \(x_0 = 3\).

Cho hàm số  \(f(x) =\left\{\begin{matrix} 3x + 2; & x<-1\\ x^{2}-1 & x \geq -1 \end{matrix}\right.\)

a) Vẽ đồ thị của hàm số \(y = f(x)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Cho hàm số  \(f(x) =\frac{x +1}{x^{2}+x-6}\) và \(g(x) = tanx + sin x\).

Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục.

Ý kiến sau đúng hay sai ?

"Nếu hàm số \(y = f(x)\) liên tục tại điểm \(x_0\) còn hàm số \(y = g(x)\) không liên tục tại x₀, thì \(y = f(x) + g(x)\) là một hàm số không liên tục tại \(x_0\)_." 

Chứng minh rằng phương trình:

a) \(2x^3 + 6x + 1 = 0\) có ít nhất hai nghiệm;

b) \(cosx = x\) có nghiệm.

Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm O của thấu kính. Công thức thấu kính là \(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}.\)

a) Tìm biểu thức xác định hàm số d' = f(d).

b) Tìm \(\underset{d\rightarrow f^{+} }{lim}φ(d)\), \(\underset{d\rightarrow f^{-} }{lim}φ(d)\) và \(\underset{d\rightarrow +\infty }{lim}φ(d)\). Giải thích ý nghĩa của các kết quả tìm được.

Hãy lập bảng liệt kê các giới hạn đặc biệt của dãy số và các giới hạn đặc biệt của hàm số.

Cho hai dãy số (u_n) và (v_n). Biết |u_n – 2| ≤ v_n với mọi n và lim v_n = 0. Có kết luận gì về giới hạn của dãy số (u_n)?

Tên của một học sinh được mã hóa bởi số 1530. Biết rằng mỗi chữ số trong số này là giá trị của một trong các biểu thức A, H, N, O với:

\(A=lim \frac{3n-1}{n+2}\)                 \(H=lim (\sqrt{n^2+2n}-n)\)

\(N=lim \frac{\sqrt{n}-2}{3n+7}\)               \(O=lim \frac{3^n-5.4^n}{1-4^n}\)

Hãy cho biết tên của học sinh này, bằng cách thay các chữ số trên bởi các ký hiệu biểu thức tương ứng.

a) Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn.

b) Cho ví dụ về cấp số nhân lùi vô hạn có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của mỗi cấp số nhân đó.

Tính các giới hạn sau

a) \(\lim_{x\rightarrow 2}\frac{x+3}{x^2+x+4}\)

b) \(\lim_{x\rightarrow -3}\frac{x^2+5x+6}{x^2+3x}\)

c) \(\lim_{x\rightarrow 4^-}\frac{2x-5}{x-4}\)

d) \(\lim_{x\rightarrow +\infty } (-x^3+x^2-2x+1)\)

e) \(\lim_{x\rightarrow -\infty } \frac{x+3}{3x-1}\)

f) \(\lim_{x\rightarrow -\infty } \frac{\sqrt{x^2-2x+4}-x}{3x-1}\)

Cho hai hàm số \(f(x)=\frac{1-x^2}{x^2}\) và \(g(x)=\frac{x^3+x^2+1}{x^2}\)

a) Tính \(\lim_{x\rightarrow 0}f(x); \lim_{x\rightarrow 0}g(x); \lim_{x\rightarrow +\infty }f(x); \lim_{x\rightarrow +\infty}g(x)\)

b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường cong nào là đồ thị của mỗi hàm số đó.

Xét tính liên tục trên \(\mathbb{R}\) của hàm số: \(g(x)=\left\{\begin{matrix} \frac{x^2-x-2}{x-2} \ neu \ x>2\\ 5-x \ \ \ \ neu \ x\leq 2 \end{matrix}\right.\)

Chứng minh rằng phương trình x⁵ – 3x⁴ + 5x – 2 = 0 có ít nhất ba nghiệm nằm trong khoảng (-2, 5).

Mệnh đề nào sau đây là mệnh đề đúng?

A. Một dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm.

B. Nếu (u_n) là dãy số tăng thì lim u_n = +∞.

C. Nếu lim u_n = +∞ và  lim v_n = +∞ thì lim (u_n – v_n) = 0.

D. Nếu u_n = aⁿ và -1< a < 0 thì lim u_n = 0.

Cho dãy số (u_n) với \(u_n=\frac{1+2+3+....+n}{n^2+1}\). Mệnh đề nào sau đây là đúng?

A. \(lim \ u_n=0\)

B. \(lim \ u_n=\frac{1}{2}\)

C. \(lim \ u_n= 1\)

D. Dãy (u_n) không có giới hạn khi \(n\rightarrow +\infty\)

Cho dãy số (u_n) với: \(u_n=\sqrt{2}+(\sqrt{2})^2+...+(\sqrt{2})^n\). Chọn mệnh đề đúng trong các mệnh đề sau:

A. \(lim \ u_n=\sqrt{2} + (\sqrt{2})^2+...+(\sqrt{2})^n+...=\frac{\sqrt{2}}{1-\sqrt{2}}\)

B. \(lim \ u_n=-\infty\)

C. \(lim \ u_n=+\infty\)

D. Dãy số (u_n) không có giới hạn khi \(n\rightarrow +\infty\)

\(\lim_{x\rightarrow 1^-}\frac{-3x-1}{x-1}\) bằng:

A. -1                 B. \(-\infty\)              C. -3             D. \(+\infty\)

Cho hàm số: \(f(x)=\frac{1-x^2}{x}\) bằng:

A. \(+\infty\)                B. 1                  C. \(-\infty\)                D. -1

Cho hàm số: \(f(x)=\left\{\begin{matrix} \frac{3-x}{\sqrt{x+1}}-2 \ \ neu \ x\neq 3\\ m \ \ \ \ \ neu \ x = 3 \end{matrix}\right.\)

Để hàm số liên tục tại x = 3 thì phải chọn m bằng bao nhiêu:

A. 4        B. -1        C. 1         D. -4

Cho phương trình: -4x³ + 4x – 1 = 0     (1)

Mệnh đề nào sau đây là mệnh đề sai

A. Hàm số f(x) = -4x³ + 4x – 1 liên tục trên \(\mathbb{R}\).

B. Phương trình (1) không có nghiệm trên khoảng \((-\infty , 1)\).

C. Phương trình (1) có nghiệm trên khoảng \((-2, 0)\).

D. Phương trình (1) có ít nhất hai nghiệm trên khoảng \((-3,\frac{1}{2})\).

Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0:

a) \(\frac{{{{\left( { - 1} \right)}^n}}}{{n + 5}}\)

b) \(\frac{{\sin n}}{{n + 5}}\)

c) \(\frac{{\cos 2n}}{{\sqrt n  + 1}}\)

Chứng minh rằng hai dãy số (u_n) và (v_n) với

\({u_n} = \frac{1}{{n\left( {n + 1} \right)}},\,\,\,{v_n} = \frac{{{{\left( { - 1} \right)}^n}\cos n}}{{{n^2} + 1}}\)

Có giới hạn 0.

Chứng minh rằng các dãy số (u_n) sau đây có giới hạn 0:

a) \({u_n} = {\left( {0,99} \right)^n}\)

b) \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{2^n} + 1}}\)

c) \({u_n} =  - \frac{{\sin \frac{{n\pi }}{5}}}{{{{\left( {1,01} \right)}^n}}}\)

Cho dãy số (u_n) với \({u_n} = \frac{n}{{{3^n}}}\)

a. Chứng minh rằng \(\frac{{{u_{n + 1}}}}{{{u_n}}} \le \frac{2}{3}\) với mọi n.

b. Bằng phương pháp qui nạp, chứng minh rằng \(0 < {u_n} \le {\left( {\frac{2}{3}} \right)^n}\) với mọi n.

c. Chứng minh rằng dãy số (u_n) có giới hạn 0.

Tìm các giới hạn sau:

a) \(\lim \left( {2 + \frac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}} \right)\)

b) \(\lim \left( {\frac{{\sin 3n}}{{4n}} - 1} \right)\)

c) \(\lim \frac{{n - 1}}{n}\)

d) \(\lim \frac{{n + 2}}{{n + 1}}\)

Tìm \(\lim u_n\) với:

a) \({u_n} = \frac{{{n^2} - 3n + 5}}{{2{n^2} - 1}}\)

b) \({u_n} = \frac{{ - 2{n^2} + n + 2}}{{3{n^4} + 5}}\)

c) \({u_n} = \frac{{\sqrt {2{n^2} - n} }}{{1 - 3{n^2}}}\)

d) \({u_n} = \frac{{{4^n}}}{{{{2.3}^n} + {4^n}}}\)

Cho dãy số (un) xác định bởi

u₁ = 10 và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) với mọi n ≥ 1

a. Chứng minh rằng dãy số (vn) xác định bởi \({v_n} = {u_n} - \frac{{15}}{4}\) là một cấp số nhân.

b. Tìm \(\lim u_n\).

Cho một tam giác đều ABC cạnh a. Tam giác A₁B₁C₁ có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A₂B₂C₂ có các đỉnh là trung điểm các cạnh của tam giác A₁B₁C₁,…, tam giác A_n+1B_n+1C_n+1 có các đỉnh là trung điểm các cạnh của tam giác A_nB_nC_n, … . Gọi p₁, p₂, ..., p_n, … và S₁, S₂, …, S_n, … theo thứ tự là chu vi và diện tích của các tam giác.

a. Tìm giới hạn của các dãy số (p_n) và (S_n).

b. Tìm các tổng p₁+p₂+...+p_n+... và S₁+S₂+...+S_n+...

Biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

a) 0,444...

b) 0,2121...

c) 0,32111...

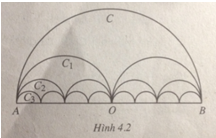
Gọi C là nửa đường tròn đường kính AB = 2R, C₁ là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2}\), C₂ là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4}\),... C­_n là đường gồm 2n nửa đường tròn đường kính \(\frac{{AB}}{{2n}}\),... (h. 4.2). Gọi p_n là độ dài của C_n, S_n là diện tích hình phẳng giới hạn bởi C­_n và đoạn thẳng AB.

a. Tính p_n và S_n.

b. Tìm giới hạn của các dãy số (p_n) và (S­_n).

Tìm giới hạn của các dãy số (u_n) với:

a) \({u_n} =  - 2{n^3} + 3n + 5\)

b) \({u_n} = \sqrt {3{n^4} + 5{n^3} - 7n} \)

Tìm giới hạn của các dãy số (u_n) với:

a) \({u_n} = \frac{{ - 2{n^3} + 3n - 2}}{{3n - 2}}\)

b) \({u_n} = \frac{{\sqrt[3]{{{n^5} - 7{n^3} - 5n + 8}}}}{{n + 12}}\)

Tìm các giới hạn sau:

a. \(lim (2n+\cos n)\)

b. \(\lim \left( {\frac{1}{2}{n^2} - 3\sin 2n + 5} \right)\)

Chứng minh rằng nếu q > 1 thì \(\lim {q^n} =  + \infty \).

Tìm giới hạn của các dãy số (u_n) với:

a) \({u_n} = \frac{{{3^n} + 1}}{{{2^n} - 1}}\)

b) \({u_n} = {2^n} - {3^n}\)

Tìm các giới hạn sau:

a) \(\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}}\)

b) \(\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}}\)

c) \(\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}}\)

d) \(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}}\)

Tìm các giới hạn sau:

a) \(\lim \left( {3{n^3} - 7n + 11} \right)\)

b) \(\lim \sqrt {2{n^4} - {n^2} + n + 2} \)

c) \(\lim \sqrt[3]{{1 + 2n - {n^3}}}\)

d) \(\lim \sqrt {{{2.3}^n} - n + 2} \)

Tìm các giới hạn sau:

a)  \(\lim \left( {\sqrt {{n^2} + n + 1}  - n} \right)\)

Hướng dẫn: Nhân và chia biểu thức đã cho với \({\sqrt {{n^2} + n + 1}  + n}\)

b) \(\lim \frac{1}{{\sqrt {n + 2}  - \sqrt {n + 1} }}\)

Hướng dẫn: Nhân tử và mẫu của phân thức đã cho với \({\sqrt {n + 2}  + \sqrt {n + 1} }\)

c) \(\lim {\rm{ }}\left( {\sqrt {{n^2} + n + 2}  - \sqrt {n + 1} } \right)\)

d) \(\lim \frac{1}{{\sqrt {3n + 2}  - \sqrt {2n + 1} }}\)

e) \(\lim \left( {\sqrt {n + 1}  - \sqrt n } \right)n\)

f) \(\lim \frac{{\sqrt {{n^2} + 1}  - \sqrt {n + 1} }}{{3n + 2}}\)

Tổng của một cấp số nhân lùi vô hạn là \(\frac{5}{3}\), tổng ba số hạng đầu tiên của nó là \(\frac{{39}}{{25}}\). Tìm số hạng đầu và công bội của cấp số đó.

Bông tuyết Vôn Kốc

Ta bắt đầu từ một tam giác đều cạnh a. Chia mỗi cạnh của tam giác ABC thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài tam giác ABC rồi xóa đáy của nó, ta được đường gấp khúc khép kín H₁. Chia mỗi cạnh H₁ thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài H₁ rồi xóa đáy của nó, ta được đường gấp khúc khép kín H₂. Tiếp tục như vậy, ta được một hình giống như bông tuyết, gọi là bông tuyết Vôn Kốc (h. 4.6).

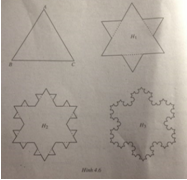
a. Gọi p₁, p₂, … , p_n, … là độ dài của H₁, H₂, … , H_n, … . Chứng minh rằng (p_n) là một cấp số nhân. Tìm \(\lim p_n\).

b. Gọi S_n là diện tích của miền giới hạn bởi đường gấp khúc H_n. Tính S_n và tìm giới hạn của dãy số (S_n).

Hướng dẫn: Số cạnh của H_n là 3.4ⁿ. Tìm độ dài mỗi cạnh của H_n, từ đó tính p_n. Để tính S_n cần chú ý rằng muốn có H_n+1 chỉ cần thêm vào một tam giác đều nhỏ trên mỗi cạnh của H_n.

Áp dụng định nghĩa giới hạn của hàm số, tìm các giới hạn sau :

a. \(\mathop {\lim }\limits_{x \to  - 1} \frac{{{x^2} - 3x - 4}}{{x + 1}}\)

b. \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {5 - x} }}\)

Cho hàm số \(f\left( x \right) = \cos \frac{1}{x}\) và hai dãy số \(\left( {x{'_n}} \right),\left( {x'{'_n}} \right)\) với:

\(x{'_n} = \frac{1}{{2n\pi }},\,\,\,\,\,\,\,\,\,x'{'_n} = \frac{1}{{\left( {2n + 1} \right)\frac{\pi }{2}}}\)

a. Tìm giới hạn của các dãy số \(\left( {x{'_n}} \right),\left( {x'{'_n}} \right),\left( {f\left( {x{'_n}} \right)} \right)\) và \(\left( {f\left( {x'{'_n}} \right)} \right)\)

b. Tồn tại hay không \(\mathop {\lim }\limits_{x \to 0} \cos \frac{1}{x}\)?

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 2} \left( {3{x^2} + 7x + 11} \right)\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{{x - {x^3}}}{{\left( {2x - 1} \right)\left( {{x^4} - 3} \right)}}\)

c) \(\mathop {\lim }\limits_{x \to 0} x\left( {1 - \frac{1}{x}} \right)\)

d) \(\mathop {\lim }\limits_{x \to 9} \frac{{\sqrt x  - 3}}{{9x - {x^2}}}\)

e) \(\mathop {\lim }\limits_{x \to \sqrt 3 } \left| {{x^2} - 4} \right|\)

f) \(\mathop {\lim }\limits_{x \to 2} \sqrt {\frac{{{x^4} + 3x - 1}}{{2{x^2} - 1}}} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{3{x^2} - x + 7}}{{2{x^3} - 1}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{2{x^4} + 7{x^3} - 15}}{{{x^4} + 1}}\)

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^6} + 2} }}{{3{x^3} - 1}}\)

d) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^6} + 2} }}{{3{x^3} - 1}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \sqrt[3]{{\frac{{{x^2} + 2x}}{{8{x^2} - x + 3}}}}\)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{x\sqrt x }}{{{x^2} - x + 2}}\)

Áp dụng định nghĩa giới hạn bên phải và giới hạn bên trái của hàm số, tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} \)

b) \(\mathop {\lim }\limits_{x \to {5^ - }} \left( {\sqrt {5 - x}  + 2x} \right)\)

c) \(\mathop {\lim }\limits_{x \to {3^ + }} \frac{1}{{x - 3}}\)

d) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}\)

Tìm các giới hạn sau (nếu có):

a. \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{\left| {x - 2} \right|}}{{x - 2}}\)

b. \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{\left| {x - 2} \right|}}{{x - 2}}\)

c. \(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\) 

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{x + 2\sqrt x }}{{x - \sqrt x }}\)

b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{4 - {x^2}}}{{\sqrt {2 - x} }}\)

c) \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 3x + 2}}{{\sqrt {{x^5} + {x^4}} }}\)

d) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {{x^2} - 7x + 12} }}{{\sqrt {9 - {x^2}} }}\)

Cho hàm số

\(f\left( x \right) = \left\{ \begin{array}{l}
2\left| x \right| - 1\,\,\,\,\,\,\,\,khi\,\,x \le  - 2\\
\sqrt {2{x^2} + 1} \,\,\,\,khi\,\,x >  - 2
\end{array} \right.\)

Tìm \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right),\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to  - 2} f\left( x \right)\) (nếu có).

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to \sqrt 3 } \left| {{x^2} - 8} \right|\)

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + x + 1}}{{{x^2} + 2x}}\)

c) \(\mathop {\lim }\limits_{x \to  - 1} \sqrt {\frac{{{x^3}}}{{{x^2} - 3}}} \)

d) \(\mathop {\lim }\limits_{x \to 3} \sqrt[3]{{\frac{{2x\left( {x + 1} \right)}}{{{x^2} - 6}}}}\)

e) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{\sqrt {1 - {x^3}}  - 3x}}{{2{x^2} + x - 3}}\)

f) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{2\left| {x + 1} \right| - 5\sqrt {{x^2} - 3} }}{{2x + 3}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \sqrt 2 } \frac{{{x^3} + 2\sqrt 2 }}{{{x^2} - 2}}\)

b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^4} - 27x}}{{2{x^2} - 3x - 9}}\)

c) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{{x^4} - 16}}{{{x^2} + 6x + 8}}\)

d) \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\sqrt {1 - x}  + x - 1}}{{\sqrt {{x^2} - {x^3}} }}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \sqrt[3]{{\frac{{2{x^5} + {x^3} - 1}}{{\left( {2{x^2} - 1} \right)\left( {{x^3} + x} \right)}}}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{2\left| x \right| + 3}}{{\sqrt {{x^2} + x + 5} }}\)

c) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^2} + x}  + 2x}}{{2x + 3}}\)

d) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {x + 1} \right)\sqrt {\frac{x}{{2{x^4} + {x^2} + 1}}} \)

Cho hàm số 

\(f\left( x \right) = \left\{ \begin{array}{l}
{x^2} - 2x + 3,\,\,\,x \le 2\\
4x - 3,\,\,\,\,\,\,\,\,\,\,\,\,\,x > 2
\end{array} \right.\)

Tìm \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) (nếu có)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {3{x^3} - 5{x^2} + 7} \right)\)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \sqrt {2{x^4} - 3x + 12} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{2x + 1}}{{x - 2}}\)

b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x + 1}}{{x - 2}}\)

c) \(\mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{x} - \frac{1}{{{x^2}}}} \right)\)

d) \(\mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{{x - 2}} - \frac{1}{{{x^2} - 4}}} \right)\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^3} - 5}}{{{x^2} + 1}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}}\)

Tính:

a) \(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{2}{{{{\left( {x - 1} \right)}^2}}}.\frac{{2x + 1}}{{2x - 3}}} \right]\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{5}{{\left( {x - 1} \right)\left( {{x^2} - 3x + 2} \right)}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 8}}{{{x^2} - 4}}\)

b) \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ + }} \frac{{2{x^2} + 5x - 3}}{{{{\left( {x + 3} \right)}^2}}}\)

c) \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{2{x^2} + 5x - 3}}{{{{\left( {x + 3} \right)}^2}}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^3} + 1}  - 1}}{{{x^2} + x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{2{x^2} + x - 10}}{{9 - 3{x^3}}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {2{x^2} - 7x + 12} }}{{3\left| x \right| - 17}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \left( {{x^3} + 1} \right)\sqrt {\frac{x}{{{x^2} - 1}}} \)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {x + 2} \right)\sqrt {\frac{{x - 1}}{{{x^3} + x}}} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + 1}  - x} \right)\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x - {x^2}}  - 1}}{{{x^2} - x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{x} + \frac{1}{{{x^2}}}} \right)\)

b) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{{x^3} + 8}}{{x + 2}}\)

c) \(\mathop {\lim }\limits_{x \to 9} \frac{{3 - \sqrt x }}{{9 - x}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{2 - \sqrt {4 - x} }}{x}\)

e) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^4} - {x^3} + 11}}{{2x - 7}}\)

f) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^4} + 4} }}{{x + 4}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \sqrt 3 } \frac{{{x^3} + 3\sqrt 3 }}{{3 - {x^2}}}\)

b) \(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{{x^2} - 4x}}\)

c) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {x - 1} }}{{{x^2} - x}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + x + 1}  - 1}}{{3x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } x\sqrt {\frac{{2{x^3} + x}}{{{x^5} - {x^2} + 3}}} \)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\left| x \right| + \sqrt {{x^2} + x} }}{{x + 10}}\)

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {2{x^4} + {x^2} - 1} }}{{1 - 2x}}\)

d) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {2{x^2} + 1}  + x} \right)\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {{x^2} + x}  - \sqrt x }}{{{x^2}}}\)

b) \(\mathop {\lim }\limits_{x \to {1^ - }} x.\frac{{\sqrt {1 - x} }}{{2\sqrt {1 - x}  + 1 - x}}\)

c) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{3 - x}}{{\sqrt {27 - {x^3}} }}\)

d) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{\sqrt {{x^3} - 8} }}{{{x^2} - 2x}}\)

Chứng minh rằng:

a. Các hàm số \(f(x)=x^3−x+3\) và \(g\left( x \right) = \frac{{{x^3} - 1}}{{{x^2} + 1}}\) liên tục tại mọi điểm x ∈ R.

b. Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^2} - 3x + 2}}{{x - 2}},\,\,\,x \ne 2\\
1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2
\end{array} \right.\) liên tục tại điểm x = 2

c. Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^3} - 1}}{{x - 1}},\,\,\,x \ne 1\\
2,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1
\end{array} \right.\) gián đoạn tại điểm x = 1

Chứng minh rằng:

a. Hàm số \(f(x)=x^4−x^2+2\) liên tục trên R

b. Hàm số \(f\left( x \right) = \frac{1}{{\sqrt {1 - {x^2}} }}\) liên tục trên khoảng (-1;1) ;

c. Hàm số \(f\left( x \right) = \sqrt {8 - 2{x^2}} \) liên tục trên đoạn [-2;2];

d. Hàm số \(f\left( x \right) = \sqrt {2x - 1} \) liên tục trên nửa khoảng \(\left[ {\frac{1}{2}; + \infty } \right)\)

Chứng minh rằng mỗi hàm số sau đây liên tục trên tập xác định của nó:

a.  \(f\left( x \right) = \frac{{{x^2} + 3x + 4}}{{2x + 1}}\)

b.  \(f\left( x \right) = \sqrt {1 - x}  + \sqrt {2 - x} \)

Chứng minh rằng phương trình :

x²cosx + xsinx + 1 = 0 có ít nhất một nghiệm thuộc khoảng (0;π).

Chứng minh rằng:

a. Hàm số

\(f\left( x \right) = \left\{ \begin{array}{l}
{\left( {x + 1} \right)^2},\,\,\,x \le 0\\
{x^2} + 2,\,\,\,\,\,\,\,x > 0
\end{array} \right.\) gián đoạn tại điểm x = 0

b. Mỗi hàm số

\(g\left( x \right) = \sqrt {x - 3} \) và \(h\left( x \right) = \left\{ \begin{array}{l}
\frac{1}{{x - 2}},\,\,\,x \le 1\\
 - \frac{1}{x},\,\,\,\,\,\,\,x > 1
\end{array} \right.\) liên tục trên tập xác định của nó.

Giải thích vì sao:

a. Hàm số \(f\left( x \right) = {x^2}\sin x - 2{\cos ^2}x + 3\) liên tục trên R.

b. Hàm số \(g\left( x \right) = \frac{{{x^3} + x\cos x + \sin x}}{{2\sin x + 3}}\) liên tục trên R

c. Hàm số \(h\left( x \right) = \frac{{\left( {2x + 1} \right)\sin x - {{\cos }^3}x}}{{x\sin x}}\) liên tục tại mọi điểm \(x \ne k\pi ,k \in Z\).

Chứng minh rằng hàm số \(f\left( x \right) = {x^2} + x + 3 + \frac{1}{{x - 2}}\) liên tục trên tập xác định của nó.

Chứng minh rằng phương trình x³+x+1 = 0 có ít nhất một nghiệm âm lớn hơn - 1.

Tìm giới hạn của các dãy số (u_n) với:

a) \({u_n} = \frac{{2{n^3} - n - 3}}{{5n - 1}}\)

b) \({u_n} = \frac{{\sqrt {{n^4} - 2n + 3} }}{{ - 2{n^2} + 3}}\)

c) \({u_n} =  - 2{n^2} + 3n - 7\)

d) \({u_n} = \sqrt[3]{{{n^9} + 8{n^2} - 7}}\)

Tìm các giới hạn của các dãy số (u_­­n) với:

a) \({u_n} = \sqrt {3n - 1}  - \sqrt {2n - 1} \)

b) \({u_n} = \frac{{{4^n} - {5^n}}}{{{2^n} + {{3.5}^n}}}\)

Cho một cấp số nhân (un), trong đó:

243u₈ = 32u₃ với u₃ ≠ 0.

a. Tính công bội của cấp số nhân đã cho.

b. Biết rằng tổng của cấp số nhân đã cho bằng 3⁵, tính u₁.

Tìm giới hạn của dãy số (u_n) xác định bởi:

\({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{n\left( {n + 1} \right)}}\).

Hướng dẫn: Với mỗi số nguyên dương k, ta có

\(\frac{1}{{k\left( {k + 1} \right)}} = \frac{1}{k} - \frac{1}{{k + 1}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - 2} \sqrt[3]{{\frac{{2{x^4} + 3x + 1}}{{{x^2} - x + 2}}}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^2} - x + 5} }}{{2x - 1}}\)

c) \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{{x^4} + 1}}{{{x^2} + 4x + 3}}\)

d) \(\mathop {\lim }\limits_{x \to 2} \frac{3}{{{{\left( {x - 2} \right)}^2}}}\sqrt {\frac{{x + 4}}{{4 - x}}} \)

e) \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{{\sqrt {8 + 2x}  - 2}}{{\sqrt {x + 2} }}\)

f) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + x}  - \sqrt {4 + {x^2}} } \right)\)

Hàm số

\(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^3} + 8}}{{4x + 8}},\,\,\,\,x \ne  - 2\\
3,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2
\end{array} \right.\)

Có liên tục trên R không ?

Tìm các giá trị của tham số m để hàm số

\(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^2} - 3x + 2}}{{{x^2} - 2x}},\,\,\,\,x < 2\\
mx + m + 1,\,\,\,\,\,\,x \ge 2
\end{array} \right.\)

Liên tục tại điểm x = 2

Chứng minh rằng phương trình:

\({x^4} - 3{x^2} + 5x - 6 = 0\)

Có ít nhất một nghiệm thuộc khoảng (1;2).

a. \(\lim \frac{{n - 2\sqrt n \sin 2n}}{{2n}}\) là :

A. 1

B. \(\frac{1}{2}\)

C. -1

D. 0

b. \(\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\) là :

A.  \(\frac{1}{2}\)$\frac{\mathrm{}}{}$

B.  \(\frac{1}{5}\)$\frac{\mathrm{}}{}$

C.  \(-\frac{3}{2}\)$\frac{\mathrm{}}{}$

D. 0

c. \(\lim \frac{{{3^n} - 1}}{{{2^n} - {{2.3}^n} + 1}}\) là :

A.  \(-\frac{1}{2}\)$\frac{\mathrm{}}{}$

B.  \(\frac{3}{2}\)$\frac{\mathrm{}}{}$

C.  \(\frac{1}{2}\)$\frac{\mathrm{}}{}$

D. -1

d. \(\lim \left( {2n - 3{n^3}} \right)\) là :

A. +∞

B. −∞

C. 2

D. -3

a. \(\lim \frac{{{n^3} - 2n}}{{1 - 3{n^2}}}\) là :

A.  \(\frac{{ - 1}}{3}\)

B.  \(\frac{2}{3}\)$\frac{\mathrm{}}{}$

C.  +∞

D.  −∞

b. \(\lim \left( {{2^n} - {5^n}} \right)\) là :

A. +∞

B. 1

C. −∞

D. \(\frac{5}{2}\)

c. \(\lim \left( {\sqrt {n + 1}  - \sqrt n } \right)\) là :

A. +∞

B. −∞

C. 0

D. 1

d. \(\lim \frac{1}{{\sqrt {{n^2} + n}  - n}}\) là :

A. +∞

B. 0

C. 2

D. -2

a. \(\lim \frac{{1 - {2^n}}}{{{3^n} + 1}}\) là :

A. \(\frac{{ - 2}}{3}\)

B. 0

C. 1

D. \(\frac{1}{2}\)

b. Tổng của cấp số nhân vô hạn

\( - \frac{1}{2},\frac{1}{4}, - \frac{1}{8},...,\frac{{{{\left( { - 1} \right)}^n}}}{{{2^n}}},...\)

Là :

A.  \(-\frac{1}{4}\)$\frac{\mathrm{}}{}$

B.  \(\frac{1}{2}\)$\frac{\mathrm{}}{}$

C. - 1

D.  \(-\frac{1}{3}\)$\frac{\mathrm{}}{}$

c. Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bởi phân số :

A.  611

B.  4690

C.  4390

D.  4790

a. Trong bốn giới hạn sau đây giới hạn nào là -1 ?

A. \(\lim \frac{{2n + 3}}{{2 - 3n}}\)

B. \(\lim \frac{{{n^2} - {n^3}}}{{2{n^3} + 1}}\)

C. \(\lim \frac{{{n^2} + n}}{{ - 2n - {n^2}}}\)

D. \(\lim \frac{{{n^3}}}{{{n^2} + 3}}\)

b. Trong bốn giới hạn sau đây, giới hạn nào là +∞ ?

A. \(\lim \frac{{{n^2} - 3n + 2}}{{{n^2} + n}}\)

B. \(\lim \frac{{{n^3} + 2n - 1}}{{n - 2{n^3}}}\)

C. \(\lim \frac{{2{n^2} - 3n}}{{{n^3} + 3n}}\)

D. \(\lim \frac{{{n^2} - n + 1}}{{2n - 1}}\)

c. Trong bốn giới hạn sau đây, giới hạn nào là 0 ?

A. \(\lim \frac{{{2^n} + 1}}{{{{3.2}^n} - {3^n}}}\)

B. \(\lim \frac{{{2^n} + 3}}{{1 - {2^n}}}\)

C. \(\lim \frac{{1 - {n^3}}}{{{n^2} + 2n}}\)

D. \(\lim \frac{{\left( {2n + 1} \right){{\left( {n - 3} \right)}^2}}}{{n - 2{n^3}}}\)