Bài tập 3 trang 141 SGK Đại số & Giải tích 11

Bài tập 3 trang 141 SGK Đại số & Giải tích 11

Câu a:

Vẽ đồ thị hàm số y=f(x).

Tập xác định của hàm số \(\mathbb{R}\)

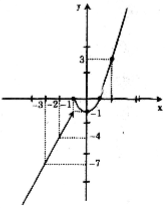
* Đồ thị f(x) = 3x+2 (với x<-1) là phần đường thẳng qua các điểm (-2;-4)(-3;-7).

* Đồ thị f(x) = x² -1 (với \(x\geq -1\)) là parabol.

* Đỉnh (0;-1)

* Bề lõm hướng lên trên.

* Cắt trục hoành tại (-1;0) và (1;0).

Căn cứ vào đồ thị ta thấy hàm số không liên tục tại điểm x= -1, liên tục trên các khoảng \((-\infty ;-1)\) và \((-1;+\infty )\).

Câu b:

Nếu \(x\geq -1\) thì \(f(x)=x^2-1.\)

Đây là hàm đa thức có tập xác định \([-1;+\infty )\) và hàm số này liên tục trên khoảng \((-1;+\infty )\).

Nếu \(x<-1\) thì \(f(x)=3x+2\)

Đây là hàm đa thức có tập xác định \((-\infty ;-1)\) nên hàm số này liên tục trên khoảng \((-\infty ;-1)\).

Mặt khác \(\lim_{x\rightarrow -1^+}f(x)=0\) và \(\lim_{x\rightarrow -1^-}f(x)=-1\) nên \(\lim_{x\rightarrow -1^+}f(x)\neq \lim_{x\rightarrow -1^-}f(x)\)

Vậy hàm số không liên tục tại x = 1.

-- Mod Toán 11

Video hướng dẫn giải bài 3 SGK