Chương 1: Hệ Thức Lượng Trong Tam Giác Vuông

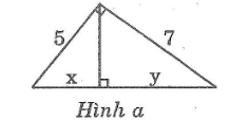
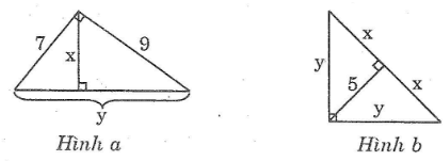
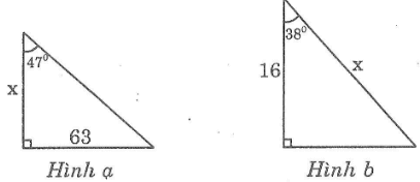
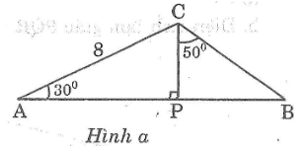
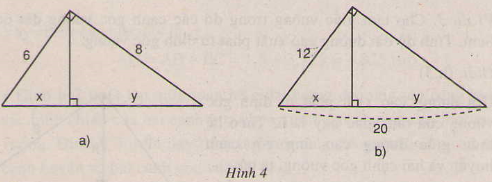
Hãy tính x và y trong mỗi hình sau (hình 4a, b):

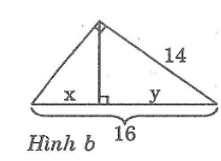
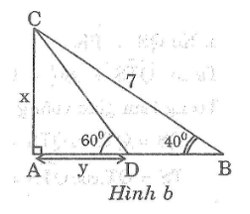
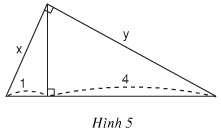
Hãy tính x và y trong hình dưới đây :

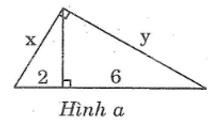
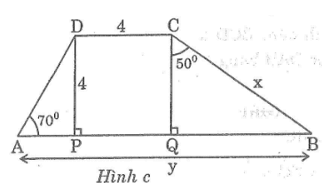
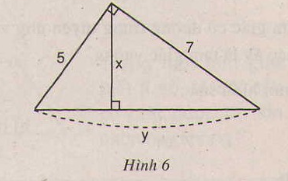
Hãy tính x và y trong hình sau (h.6)

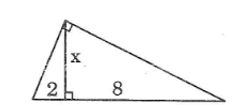
Hãy tính x và y trong hình sau:

Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.

Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x² = ab) như trong hai hình sau:

Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

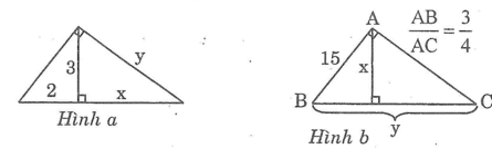
Tìm x và y trong mỗi hình sau:

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và Tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng

a) Tam giác DIL là một tam giác cân;

b) Tổng \(\frac{1}{{D{I^2}}} + \frac{1}{{D{K^2}}}\) không đổi khi I thay đổi trên cạnh AB.

Vẽ một tam giác vuông có một góc nhọn 34⁰ rồi viết các tỉ số lượng giác của góc 340

Cho tam giác ABC vuông tại C, trong đó \(AC= 0,9 m\), \(BC=1,2 m\). Tính các tỷ số lượng giác của góc B, từ đó suy ra các tỷ số lượng giác của góc A.

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45⁰: \(sin 60^{\circ},cos75^{\circ}, sin52^{\circ}30', cotg82^{\circ}, tg80^{\circ}.\)

Dựng góc nhọn \(\alpha\) , biết:

a) \(sin\alpha =\frac{2}{3}\)

b) \(cos\alpha =0,6\)

c) \(\tan \alpha  = \frac{3}{4}\)

d) \(cotg\alpha  = \frac{3}{2}\)

Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn  tùy ý, ta có:

a) \(tg\alpha =\frac{sin\alpha }{cos\alpha}\)                                \(cotg\alpha =\frac{cos\alpha }{sin\alpha }\)                                 \(tg\alpha.cotg\alpha =1\)

b) \(sin{\alpha ^2} + \cos{\alpha ^2} = 1\)

Gợi ý: Sử dụng định lý Py-ta-go.

Cho tam giác ABC vuông tại A. Biết \(cosB=0,8\); hãy tính các tỷ số lượng giác của góc C.

Gợi ý: sử dụng bài tập 14.

Cho tam giác vuông có một góc bằng 60⁰ và cạnh huyền có độ dài bằng 8. Hãy tìm độ dài của cạnh đối diện góc 600.

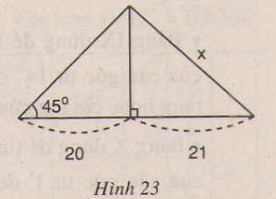
Tìm giá trị của x trong hình 23:

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn tới chữ số thập phân thứ tư):

a) \(sin{40^0}{12'}\) 

b) \(cos {52^0}{54'}\)

c) \(tg {63^0}{36'}\)

d) \(cotg {25^0}{18'}\) 

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:

a) \(sinx=0,2368\)

b) \(cosx=0,6224\)

c) \(tgx= 2,154\)

d) \(cotgx=3,251\)

Dùng bảng lượng giác (có sử dụng phần hiệu chỉnh) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư) :

a) \(sin{70^0}{13'}\)

b) \(cos25^{\circ}32'\)

c) \(tg43^{\circ}10'\)

d) \(cotg32^{\circ}15'\)

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ), biết rằng:

a) \(sinx=0,3495\)

b) \(cosx=0,5427\)

c)  \(tgx=1,5142\)

d) \(cotgx=3,163\)

So sánh: 

a) \(sin 20^{\circ}\) và \(sin70^{\circ}\)

b) \(cos25^{\circ}\) và \(cos63^{\circ}15'\)

c) \(tg73^{\circ}20'\) và \(tg45^{\circ}\) 

d) \(cotg2^{\circ}\) và \(cotg37^{\circ}40'\) 

Tính: 

a) \(\frac{sin25^{\circ}}{cos65^{\circ}}\)

b) \(tg 58^{\circ}-cotg32^{\circ}\)

Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần :

a) \(sin 78^{\circ}, cos14^{\circ}, sin47^{\circ},cos87^{\circ}\)

b) \(tg{73^0},cotg{25^0},tg{62^0},cotg{38^0}\)

So sánh:

a) \(tan25^o\) và \(sin25^o\)

b) \(cot32^o\) và \(cos32^o\)

c) \(tan45^o\) và \(cos45^o\)

d) \(cot60^o\) và \(sin30^o\)

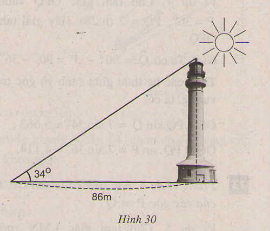
Các tia nắng mặt trời tạo với mặt đất một góc xáp xỉ bằng 34⁰ và bóng của một tháp trên mặt đất dài 86m (H.30). Tính chiều cao của tháp (làm tròn đến mét)

Giải tam giác ABC vuông tại A, biết rằng:

a) \(b=10cm; \widehat{C}=30^{\circ}\)

b) \(c=10cm; \widehat{C}=45^{\circ}\)

c) \(a=20cm; \widehat{B}=35^{\circ}\) 

d) c = 21cm; b = 18cm

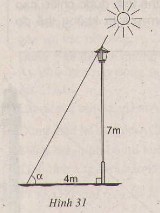
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc \(\alpha \) trong hình 31).

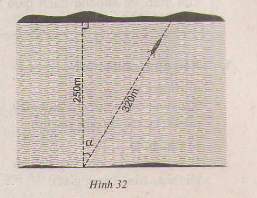
Một khúc sông sộng khoảng 250m. Một chiếc thuyền chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu độ? (góc \(\alpha\) trong hình 32).

Cho tam giác ABC, trong đó BC=11cm, \(\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}.\) Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính:

a) Đoạn thẳng AN

b) Cạnh AC

Gợi ý: Kẻ BK vuông góc với AC.

Trong hình 33

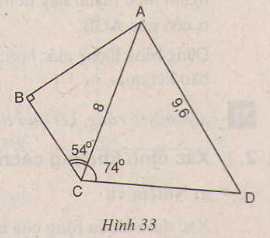
\(AC=8cm, AD=9,6cm, \widehat{ABC}=90^{\circ}, \widehat{ACD}=74^{\circ}.\)

Hãy tính:

a) AB;

b) \(\widehat {ADC}\)

Một con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một góc 70 độ. Từ đó ta tính được chiều rộng của khúc sông chưa? Nếu có thể hãy tính kết quả (làm tròn đến mét)

Hãy tính x và y trong các hình sau:

Hãy tính x và y trong các hình sau:

Hãy tính x và y trong các hình sau:

Hãy tính x và y trong các hình sau:

Cho tam giác ABC vuông tại A, đường cao AH. Giải bài toán trong mỗi trường hợp sau:

a. Cho AH = 16, BH = 25. Tính AB, AC, BC, CH

b. Cho AB = 12, BH = 6. Tính AH, AC, BC, CH

Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.

Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của tam giác này.

Cạnh huyển của một tam giác vuông lớn hơn một cạnh góc vuông là 1 cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyển là 4cm. Hãy tính các cạnh của tam giác vuông này.

Một tam giác vuông có cạnh huyền là 5 và đường cao tương ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.

Cho một tam giác vuông. Biết tỉ số hai cạn góc vuông là 3 : 4 và cạnh huyền là 125 cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.

Cho tam giác ABC vuông tại A. Biết rằng \(\frac{{AB}}{{AC}} = \frac{5}{6}\) , đường cao AH = 30cm. Tính HB, HC.

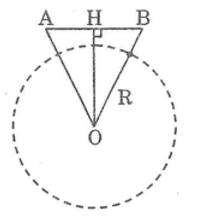
Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đấy 230 km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200 km? Biết rằng bán kính R của Trái Đất gần bằng 6370 km và hai vệ tinh nhìn thấy nhau nếu OH > R.

Cho hai đoạn thẳng có độ dài là a và b. Dựng các đoạn thẳng có độ dài tương ứng bằng:

\(\begin{array}{l}
a)\sqrt {{a^2} + {b^2}} \\
b)\sqrt {{a^2} - {b^2}} \left( {a > b} \right)
\end{array}\)

Cho hai đoạn thẳng có độ dài là a và b. Dựng đoạn thẳng \(\sqrt {ab} \) như thế nào?

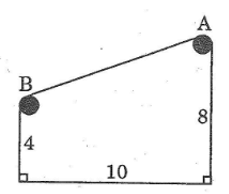
Giữa hai tòa nhà (kho và phân xưởng) của một nhà máy, người ta xây dựng một băng chuyền AB để chuyển vật liệu. Khoảng cách giữa hai tòa nhà là 10m, còn hai vòng quay của băng chuyền được đặt ở độ cao 8m và 4m so với mặt đất. Tìm độ dài AB của băng chuyền.

Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc đối diện với cạnh có độ dài 13 của tam giác.

Cho hình chữ nhật ABCD. Đường phân giác của góc B cắt đường chéo AC thành hai đoạn \(4\frac{2}{7}m\) và \(5\frac{5}{7}m\). Tính các kích thước của hình chữ nhật.

Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Chu vi của tam giác ABH là 30cm và chu vi của tam giác ACH là 40cm. Tính chu vi của tam giác ABC.

Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.

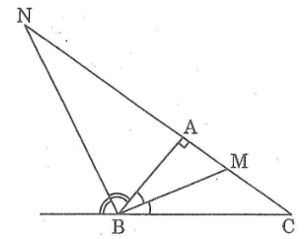
Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kẻ MD, ME, MF lần lượt vuông góc với các cạnh BC, AC, AB. Chứng minh rằng: BD² + CE² + AF² = DC² + EA² + FB²

Cho tam giác ABC vuông tại A. Chứng minh rằng \(\frac{{AB}}{{AC}} = \frac{{\sin \widehat B}}{{\sin \widehat C}}\)

Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α

Biết tg α = 5/12 . Hãy tính:

a. Cạnh AC     

b. Cạnh BC

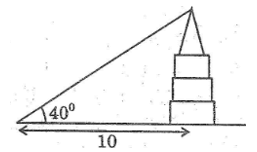
Tìm giá trị của x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình sau, biết:

tg47⁰ ≈ 1,072, cos38⁰ ≈ 0,788

Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.

Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:

a. AB = 13, BH = 5     

b. BH = 3, CH = 4

Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn 450: sin75⁰, cos530, sin47020’, tg620, cotg82045’

Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính:

a) \(\frac{{\sin {{32}^0}}}{{\cos {{58}^0}}}\)

b) tg76⁰ – cotg14⁰

Đường cao MQ của tam giác vuông MNP chia cạnh huyển NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg\(\widehat N\) và cotg \(\widehat P\) . Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?

Cạnh góc vuông kề với góc 60⁰ của một tam giác vuông bằng 3. Sử dụng bảng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư)

Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.

a. Tính diện tích tam giác ABD

b. Tính AC, dùng các thông tin dưới đây nếu cần:

\(\sin \widehat C = \frac{3}{5};\cos \widehat C = \frac{4}{5};tan\widehat C = \frac{3}{4}\)

Cho cos α = 0,8. Hãy tìm sin α, tg α, cotg α (làm tròn đến chữ số thập phân thứ tư)

Hãy tìm sin α, cos α (làm tròn đến chữ số thập phân thứ tư) nếu biết:

a. tg α = 1/3     

b. cotg α = 3/4

 Dựng góc nhọn α, biết rằng:

a. sin α = 0,25    

b. cos α = 0,75

c. tg α = 1    

d. cotg α = 2

Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1; 1), B(5; 1), C(7; 9)

Hãy tính:

a. Giá trị của tg\(\widehat {BAC}\) (làm tròn đến chữ số thập phân thứ tư)

b. Độ dài của cạnh AC

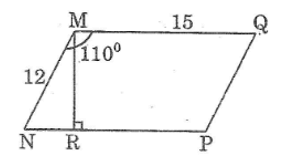
Cho hình dưới. Hãy viết một phương trình để từ đó có thể tìm được x (không phải giải phương trình này).

Cho hình bên dưới. Hãy tính sin\(\widehat L\) (làm tròn đến chữ số thập phân thứ tư), biết rằng sin30⁰ = 0,5.

Tìm đẳng thức đúng

A. \(\sin \alpha  = \frac{a}{b}\)

B. \(\sin \alpha  = \frac{b}{c}\)

C. \(\sin \alpha  = \frac{b'}{b}\)

D. \(\sin \alpha  = \frac{h}{a}\)

Tìm đẳng thức đúng

A. \(\cos \alpha  = \frac{a}{b}\)

B. \(\cos \alpha  = \frac{a}{c}\)

C. \(\cos \alpha  = \frac{b}{c}\)

D. \(\cos \alpha  = \frac{b'}{b}\)

A. \(tg\alpha  = \frac{b}{a}\)

B. \(tg\alpha  = \frac{b}{c}\)

C. \(tg\alpha  = \frac{b}{h}\)

D. \(tg\alpha  = \frac{h}{b'}\)

Tìm đẳng thức đúng

A. \({\mathop{\rm cotg}\nolimits} \alpha  = \frac{b}{a}\)

B. \({\mathop{\rm cotg}\nolimits} \alpha  = \frac{b}{c}\)

C. \({\mathop{\rm cotg}\nolimits} \alpha  = \frac{a}{c}\)

D. \({\mathop{\rm cotg}\nolimits} \alpha  = \frac{h}{b}\)

Tìm đẳng thức đúng

A. sinα = sinβ;       

B. sinα = cosβ;

C. sinα = tgβ;       

D. sinα = cotgβ.

Tìm đẳng thức đúng

A. cosα = cosβ;       

B. cosα = tgβ;

C. cosα = cotgβ;       

D. cosα = sinβ.

Tìm đẳng thức đúng

A. tgα = tgβ;       

B. tgα = cotgβ;

C. tgα = sinβ;       

D. tgα = cosβ

Tìm đẳng thức đúng

A. cotgα = tgβ;       

B. cotgα = cotgβ;

C. cotgα = cosβ;       

D. cotgα = sinβ;

Tìm đẳng thức đúng

A. cos² α + sin22 β = 1;       

B. sin2 α + cos2 β = 1;

C. cos2 α + sin2 α = 1;       

D. cos2 α + sin2 β = 2.

Tìm đẳng thức đúng

A. tgα = sinα + cosα;       

B. tgα = sinα - cosα;

C. tgα = sinα. cosα;       

D. tgα = sinα/cosα.

Tìm đẳng thức đúng

A. cotgα = 1 + tgα;       

B. cotgα = 1 - tgα;

C. cotgα = 1. tgα;       

D. cotgα = 1/tgα.

Cho sinα = 1/2. Hãy tìm cosα, tgα, cotgα (00< α < 90⁰).

Cho cosα = \(\frac{3}{4}\). Hãy tìm sinα, tgα, cotgα (00 < α < 90⁰).

Cho tam giác ABC vuông tại A, có AB = \(\frac{1}{3}\)BC. Hãy tính sinC, cosC, tgC, cotgC.

Hãy tính

a) 2sin30⁰ - 2cos600 + tg45⁰;

b) sin450 + cotg600.cos300;

c) cotg440.cotg450.cotg460.

Cho tam giác ABC có \(\widehat A = {60^0}\). Chứng minh rằng: BC² = AB2 + AC2 – AB.AC.

Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng S_ABCD = \(\frac{1}{2}\) AC.BD.sinα.

Cho góc nhọn α

a) Chứng minh rằng: \(\frac{{1 - tg\alpha }}{{1 + tg\alpha }} = \frac{{\cos \alpha  - \sin \alpha }}{{\cos \alpha  + \sin \alpha }}\)

b) Cho \(tg\alpha  = \frac{1}{3}\). Chứng minh \(\frac{{\cos \alpha  - \sin \alpha }}{{\cos \alpha  + \sin \alpha }}\)

Tính giá trị của biểu thức

a) \(\frac{{3{\mathop{\rm cotg}\nolimits} {{60}^0}}}{{2{{\cos }^2}{{30}^0} - 1}}\)

b) \(\frac{{\cos {{60}^0}}}{{1 + \sin {{60}^0}}} + \frac{1}{{tg{{30}^0}}}\)

Trong hình thang vuông ABCD với các đáy AD, BC có ∠A = ∠B = 90⁰, ∠(ACD) = 900. BC = 4cm, AD = 16cm. Hãy tìm các góc C và D của hình thang.

Tính các góc của một hình thoi, biết hai đường chéo của nó có độ dài là 2\(\sqrt 3 \) và 2.

Các cạnh của một hình chữ nhật bằng 3cm và \(\sqrt 3 \) cm. Hãy tìm các góc hợp bởi đường chéo và các cạnh của hình chữ nhật đó.

Cho tam giác ABC vuông tại A có AB : AC = 3 : 4 và đường cao AH bằng 9cm. Khi đó độ dài đoạn thẳng HC bằng

A. 6cm;       

B. 9cm;       

C. 12cm;       

D. 15cm.

Hãy chọn phương án đúng

Cho tam giác ABC vuông tại A có AB : AC = 4 : 5 và đường cao AH bằng 12cm. Khi đó độ dài đoạn thẳng HB bằng

A. 6cm;       

B. 9,6cm;       

C. 12cm;       

D. 15cm.

Hãy chọn phương án đúng.

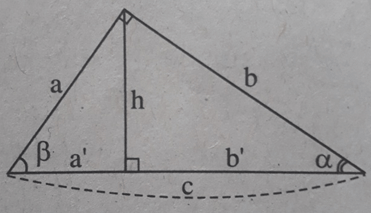
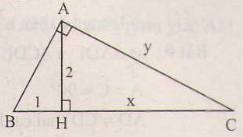
*Trong các bài (1.3, 1.4, 1.5) ta sẽ sử dụng các kí hiệu sau đây đối với tam giác ABC vuông tại A có đường cao AH:

AB = c, AC = b, BC = a, AH = h, BH = c’, CH = b'

a) Tính h, b, c nếu biết b’ = 36, c’ = 64.

b) Tính h, b, b’, c’ nếu biết a = 9, c = 6.

Hãy biểu thị b’, c’ qua a, b, c.

Chứng minh rằng:

a) \(h = \frac{{bc}}{a}\)

b) \(\frac{{{b^2}}}{{{c^2}}} = \frac{{b'}}{{c'}}\)

Đường cao của một tam giác vuông kẻ từ đỉnh góc vuông chia cạnh huyền thành hai đoạn, trong đó đoạn lớn bằng 9cm. Hãy tính cạnh huyền của tam giác vuông đó nếu hai cạnh góc vuông có tỉ lệ 6:5.

Trong tam giác có các cạnh là 5cm, 12cm, 13, kẻ đường cao đến cạnh lớn nhất. Hãy tính các đoạn thẳng mà đường cao này chia ra trên cạnh lớn nhất đó.

Tam giác ABC vuông tại A có đường cao AH bằng 12cm. Hãy tính cạnh huyền BC nếu biết HB : HC = 1 : 3.

Cho tam giác ABC vuông cân tại A, đường trung tuyến BM. Gọi D là chân đường vuông góc kẻ từ C đến BM và H là chân đường vuông góc kẻ từ D đến AC. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?

a) ΔHCD ∼ ΔABM.

b) AH = 2HD.

Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm:

sin39⁰13’; cos52018’; tg13020’; cotg10017’; sin450; cos450

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x:

a. sinx = 0,5446    

b. cosx = 0,4444    

c. tgx = 1,1111

Có góc nhọn x nào mà:

a. sinx = 1,0100    

b. cosx = 2,3540    

c. tgx = 1,6754

Cho hình dưới, biết: AB = 9cm, AC = 6,4cm, AN = 3,6cm, \(\widehat {AND} = {90^0};\widehat {DAN} = {34^0}\). Hãy tính:

a. CN

b. \(\widehat {ABN}\)

c. \(\widehat {CAN}\)

d. AD

 Cho hình bên, biết: góc (ACE) = 90⁰, AB = BC = CD = DE = 2cm. Hãy tính:

a. AD, BE

b. góc (DAC)

c. góc (BXD)

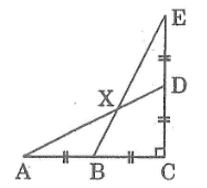
Đoạn thẳng LN vuông góc với đoạn thẳng AB tại trung điểm N của AB; M là một điểm của đoạn thẳng LN và khác với L, N. Hãy so sánh các góc (LAN) và góc (MBN)

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh:

a. sin250 và sin75⁰  

b. cos40⁰ và cos750

c. sin38⁰ và cos38⁰   

d. sin500 và cos500

Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh

a. tg50⁰28’ và tg63⁰     

b. cotg140 và cotg35012’

c. tg270 và cotg270     

d. tg650và cotg650

Cho x là một góc nhọn, biểu thức sau đây có giá trị âm hay dương? Vì sao?

a. sinx – 1    

b. 1 – cosx

c. sinx – cosx    

d. tgx – cotgx

 Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh:

a. tg280 và sin28⁰     

b. cotg420 và cos420

c. cotg730 và sin170     

d. tg320 và cos580

Tam giác ABC vuông tại A, có AC = \(\frac{1}{2}\).BC. Tính \(\sin \widehat B,cos\widehat B,tg\widehat B,\cot g\widehat B\)

Tính các góc của tam giác ABC, biết AB = 3cm, AC = 4cm và BC = 5cm

Để vẽ một tam giác cân có góc ở đáy 50⁰ mà không có thước đo góc, một học sinh vẽ một tam giác cân có cạnh bên là 3cm, cạnh đáy 4cm. Tính góc ở đáy mà em học sinh đó đã vẽ. Sai số so với số đo phải vẽ là bao nhiêu?

Hãy so sánh

a) sinα và tgα (0o < α < 90⁰);

b) cosα và cotgα ((0o < α < 900);

c) sin350 và tg380;

d) cos330 và tg610

Không tính giá trị cụ thể, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn

a) sin200, cos200, sin550, cos400, tg70⁰.

b) tg700, cotg600, cotg650, tg500, sin250

Trong tam giác vuông có một cạnh góc vuông bằng b, góc đối diện với nó bằng β.

a) Hãy biểu thị cạnh góc vuông kia, góc đối diện với cạnh này và cạnh huyền qua b và β.

b) Hãy tìm các giá trị của chúng khi b = 10cm, β = 50° (làm tròn kết quả đến chữ số thập phân thứ ba).

Trong tam giác vuông có một cạnh góc vuông bằng b, góc nhọn kề với nó bằng α.

a) Hãy biểu thị cạnh góc vuông kia, góc nhọn kề với cạnh này và cạnh huyền qua b và α.

b) Hãy tìm các giá trị của chúng khi b = 12cm, α = 42⁰ (làm tròn kết quả đến chữ số thập phân thứ ba).

Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.

Tam giác ABC vuông tại A có AB = 21cm, góc C = 40⁰. Hãy tính các độ dài:

a. AC    

b. BC    

c. Phân giác BD

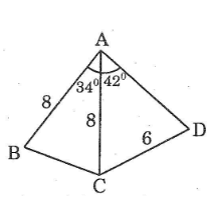
Cho hình bên. Biết AB = AC = 8cm, CD = 6cm, \(\widehat {BAC} = {34^0},\widehat {CAD} = {42^0}\)

Hãy tính:

a. Độ dài cạnh BC

b. góc (ADC)

c. Khoảng cách từ điểm B đến cạnh AD

Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, góc (BAC) = 200

Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần:

sin200 ≈ 0,3420; cos200 ≈ 0,9397; tg20⁰ ≈ 0,3640

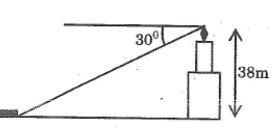
Từ đỉnh một ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 30⁰ so với đường nằm ngang chân đèn (hình bên). Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?

Trong tam giác ABC có AB = 11cm, \(\widehat {ABC} = {38^0},\widehat {ACB} = {30^0}\) , N là chân đường vuông góc kẻ từ A đến BC. Hãy tính AN, AC

Để nhìn thấy đỉnh A của một vách đá dựng đứng, người ta đã đứng tại điểm P cách chân vách đá một khoảng 45m và nhìn lên một góc 25⁰ so với đường nằm ngang (góc nhìn lên này được gọi là góc “nâng”). Hãy tính độ cao của vách đá.

Tìm x và y trong các hình sau:

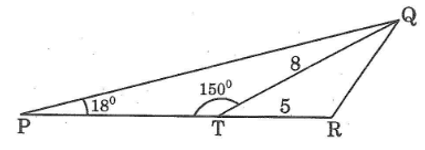
Cho hình dưới.

Biết: \(\widehat {QPT} = {18^0},\widehat {PTQ} = {150^0}\) , QT = 8cm, TR = 5cm. Hãy tính:

a. PT

b. Diện tích tam giác PQR

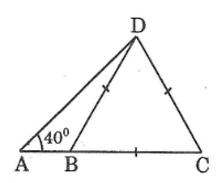
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40⁰. Hãy tính:

a. AD     

b. AB

 Cho tam giác ABC vuông tại A, đường cao AH.

Biết HB = 25cm, HC = 64cm. Tính góc B , C

Cho tam giác ABC có BC = 12cm, góc B = 60⁰, góc C = 40⁰. Tính:

a. Đường cao CH và cạnh AC

b. Diện tích tam giác ABC

Tính diện tích của hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 110⁰

Một cột cờ cao 3,5m có bóng trên mặt đất dài 4,8m. Hỏi góc giữa tia sáng mặt trời và bóng cột cờ là bao nhiêu?

Từ đỉnh một tòa nhà cao 60m, người ta nhìn thấy một chiếc ô tô đang đỗ dưới một góc 28⁰ so với đường ngang. Hỏi chiếc ô tô đang đỗ cách tòa nhà đó bao nhiêu mét?

Một em học sinh đang đứng ở cách mặt đất tháp ăng-ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20⁰ so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tháp.

Hai cột thẳng đứng của hai trại A và B (của lớp 9A và lớp 9B) cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35⁰ và 30⁰. Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?

Một người trinh sát đứng cách một tòa nhà khoảng 10m. Góc “nâng” từ chỗ anh ta đứng đến nóc tòa nhà là 40⁰ (hình bên)

a. Tính chiều cao của tòa nhà

b. Nếu anh ta dịch chuyển sao cho góc “nâng” là 35⁰ thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh ta tiến lại gần hay ra xa ngôi nhà?

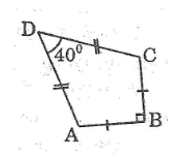
Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, \(\widehat {ADC} = {40^0},\widehat {ABC} = {90^0}\) (hình bên). Hãy tính:

a. Chiều dài cạnh AD.

b. Diện tích của chiếc diều.

Trong tam giác vuông có hai cạnh góc vuông là a, b; góc đối diện với cạnh a là α; góc đối diện với cạnh b và β và cạnh huyền là c. Hãy tìm khẳng định đúng

A. a = csinα;       

B. a = ccosα;

C. a = ctgα;       

D. a = ccotgα.

Trong tam giác vuông có hai cạnh góc vuông là a, b; góc đối diện với cạnh a là α; góc đối diện với cạnh b và β và cạnh huyền là c. Hãy tìm khẳng định đúng

A. a = csinβ;       

B. a = ccosβ;

C. a = ctgβ;       

D. a = ccotgβ.

 Trong tam giác vuông có hai cạnh góc vuông là a, b; góc đối diện với cạnh a là α; góc đối diện với cạnh b và β và cạnh huyền là c. Hãy tìm khẳng định đúng

A. a = bsinα;       

B. a = bcosα;

C. a = btgα;       

D. a = bcotgα.

 Trong tam giác vuông có hai cạnh góc vuông là a, b; góc đối diện với cạnh a là α; góc đối diện với cạnh b và β và cạnh huyền là c. Hãy tìm khẳng định đúng

A. a = bsinβ;       

B. a = bcosβ;

C. a = btgβ;       

D. a = bcotgβ.

Hãy tìm diện tích của tam giác cân có góc ở đấy bằng α nếu biết:

a) Cạnh bên bằng b;

b) Cạnh đáy bằng a.

Trong hình thang ABCD, tổng của hai đáy AD và BC bằng b, đường chéo AC bằng a, góc ACB bằng α. Hãy tìm diện tích của hình thang đó.

Cho tam giác ABC có BC = 7, ∠(ABC) = 42⁰, ∠(ACB) = 35⁰. Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH (làm tròn kết quả đến chữ số thập phân thứ ba).

Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng

\(\begin{array}{l}
a){S_{MNP}} = \frac{1}{2}MP.NP.\sin \widehat P\\
b)DP = \frac{{MN.\sin \widehat N}}{{tg\widehat P}}
\end{array}\)

c) ΔDNE ∼ ΔMNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P

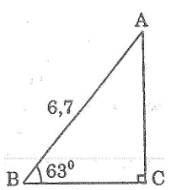
Bài toán cái thang

Thang AB dài 6,7m tựa vào tường làm thành góc 63⁰ với mặt đất. Hỏi chiều cao của cái thang đạt được so với mặt đất?

Bài toán cột cờ

Làm dây kéo cờ: Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ (chiếu bởi ánh sánh mặt trời) dài 11,6m và góc nhìn mặt trời là 36o50’

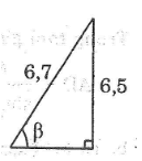
Bài toán con mèo

Một conmèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó, khi đó góc của thang so với mặt đất là bao nhiêu, biết chiếc thang dài 6,7m?

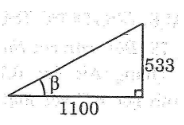
Bài toán đài quan sát

Đài quan sát ở Toronto, Ontario, Canada cao 533m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo thành bóng dài 1100m. Hỏi lúc đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu?

Bài toán hải đăng

Một người quan sát ở đài hải đăng cao 80 feet (đơn vị đo lường Anh) so với mặt nước biển, nhìn một chiếc tàu ở xa với góc 0⁰42’. Hỏi khoảng cách từ tàu đến chân hải đăng tính theo đơn vị hải lí là bao nhiêu? (1 hải lí = 5280 feet) (hình dưới)

Bài toán máy bay hạ cánh

Một máy bay đang bay ở độ cao 10km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a. Nếu phi công muốn tạo góc nghiêng 3⁰ thì cách sân bay bao nhiêu ki-lô-mét phải bắt đầu cho máy bay hạ cánh?

b. Nếu cách sân bay 300km, máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu?

Bài toán chiếu xạ chữa bệnh

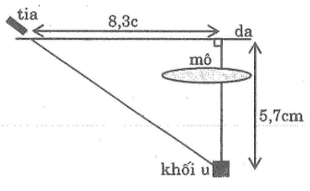
Một khối u của một bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đã đặt nguồn tia cách khối u (trên mặt da) 8,3cm (hình bên)

a. Hỏi góc tạo bởi chùm tia với mặt da?

b. Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?

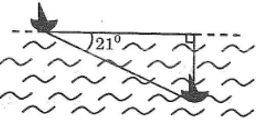
Bài toán tàu ngầm

Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc 210 (hình bên)

a. Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ saau bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu?

b. Tàu phải chạy bao nhiêu mét để đạt đến độ sâu 1000m?

Mô tả cánh của một máy bay. Hãy tính các độ dài AC, BD, AB của cánh máy bay theo các số liệu được cho trong hình đó.

Hãy tính sin α và tg α nếu:

a. cos α = 5/13    

b. cos α = 15/17    

c. cos α = 0,6

Hãy đơn giản các biểu thức:

a. 1 – sin²α    

b. (1 - cos α)(1 + cos α)

c. 1 + sin2α + cos2α    

d. sin α - sin α cos2α

e. sin4α + cos4α + 2sin2α cos2α    

g. tg2α – sin2α tg2α

h. cos2α + tg2α cos2α    

i. tg2α.(2cos2α + sin2α – 1)

Trong một tam giác với các cạnh có độ dài 6, 7, 9, kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó.

Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu đường cao kẻ xuống đáy có độ dài là 5 và đường cao kẻ xuống cạnh bên có độ dài là 6.

Tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC

a. Chứng minh DE/DB = DB/DC

b. Chứng minh tam giác BDE đồng dạng tam giác CDB

c. Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng 2 cách:

Cách 1: Sử dụng kết quả ở câu b

Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác

Tính góc α tạo bởi hai mái nhà, biết rằng mỗi mái nhà dài 2,34m và cao 0,8m

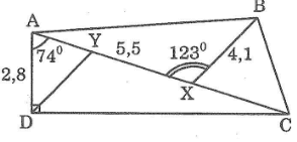
Cho hình bên.

Biết AD ⊥ DC, \(\widehat {DAC} = {74^0};\widehat {AXB} = {123^0}\) , AD = 2,8cm, AX = 5,5cm, BX = 4,1cm.

a. Tính AC

b. Gọi Y là điểm trên AX sao cho DY // BX. Hãy tính XY

c. Tính diện tích tam giác BCX

Tam giác ABC có \(\widehat A = {20^0};\widehat B = {30^0}\) , AB = 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm:

a. CP    

b. AP, BP

Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết khoảng cách giữa hai người này là 300m, góc “nâng” để nhìn thấy máy bay tại vị trí A là 400 và tại vị trí B là 30⁰ (hình bên). Hãy tìm độ cao của máy bay

 Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm, góc tù bằng 120⁰. Tính chu vi và diện tích hình thang đó.

Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm.

a. Tính BC, góc B , góc C

b. Phân giác của góc A cắt BC ở D. Tính BD, CD

c. Từ D kẻ DE và DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích tứ giác AEDF

Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC

Biết AD = 5a, AC = 12a

a. Tính \(\frac{{\sin \widehat B + \cos \widehat B}}{{\sin \widehat B - \cos \widehat B}}\)

b. Tính chiều cao của hình thang ABCD

Cho tam giác ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho AI =\(\frac{1}{3}\).AH. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D

a. Tính các góc của tam giác ABC

b. Tính diện tích tứ giác ABCD

Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm.

a. Chứng minh tam giác ABC vuông

b. Tính sin\({\widehat B}\), sin\({\widehat C}\)

 Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, góc A = 90⁰

a. Chứng minh tg\({\widehat C}\) = 1

b. Tính tỉ số diện tích tam giác BCD và diện tích hình thang ABCD

c. Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD

Cho tam giác ABC có góc B bằng 120⁰, BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D.

a. Tính độ dài đường phân giác BD

b. Gọi M là trung điểm của BC. Chứng minh AM ⊥ BD

Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC

a. Tính độ dài đoạn thẳng DE

b. Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH

c. Tính diện tích tứ giác DENM

Cho tam giác ABC vuông ở A, góc C = 30⁰, BC = 10cm

a. Tính AB, AC

b. Từ A kẻ AM, AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B. Chứng minh MN // BC và MN = AB

c. Chứng minh hai tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a. Chứng minh tam giác ABC vuông ở A. Tính các góc B, C và đường cao AH của tam giác

b. Tìm tập hợp các điểm M sao cho S_ABC = S_BMC

Tam giác ABC có \(\widehat A = {105^0};\widehat B = {45^0}\), BC = 4cm. Tính độ dài các cạnh AB, AC.

Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).

Cho tam giác ABC cân tại A, đường cao BH. Hãy tính góc A và các cạnh AB, BC, nếu biết BH = h, \(\widehat C = \alpha \)

Hình bình hành ABCD có \(\widehat A = {120^0}\), AB = a, BC = b. Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ.

Cho tam giác ABC vuông tại C có ∠B = 37⁰. Gọi I là giao điểm của cạnh BC với đường trung trực của AB. Hãy tính AB, AC nếu biết BI = 20.