Trang chủ Lớp 9 Toán Lớp 9 SGK Cũ Chương 1: Hệ Thức Lượng Trong Tam Giác Vuông Bài tập 4.8 trang 117 SBT Toán 9 Tập 1

Bài tập 4.8 trang 117 SBT Toán 9 Tập 1

Lý thuyết Bài tập
Câu hỏi:

Bài tập 4.8 trang 117 SBT Toán 9 Tập 1

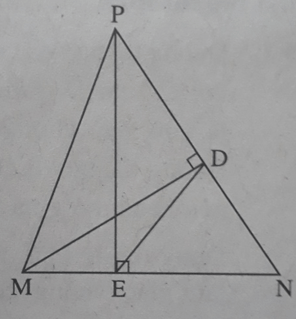
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng

\(\begin{array}{l}
a){S_{MNP}} = \frac{1}{2}MP.NP.\sin \widehat P\\
b)DP = \frac{{MN.\sin \widehat N}}{{tg\widehat P}}
\end{array}\)

c) ΔDNE ∼ ΔMNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

a) Ta có MD = MPsinP, suy ra SMNP = 1/2.NP.MD = 1/2.NP.MP.sinP.

b) Ta có MD = MN.sinN và MD = DP.tgP nên từ đó suy ra

c) Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên  Hai tam giác DNE và MNP đồng dạng vì có góc N chung và 

 

-- Mod Toán 9

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Copyright © 2021 HOCTAP247