Chương 1: Vectơ

Cho ba vectơ \(\vec a,\vec b,\vec c\)  đều khác vec tơ  \(\vec 0\). Các khẳng định sau đây đúng hay sai?

a) Nếu hai vectơ \(\vec a,\vec b\) cùng phương với \(\vec c\) thì \(\vec a,\vec b\) cùng phương.

b) Nếu \(\vec a,\vec b\)  cùng ngược hướng với \(\vec c\) thì \(\vec a\) và \(\vec b\) cùng hướng .

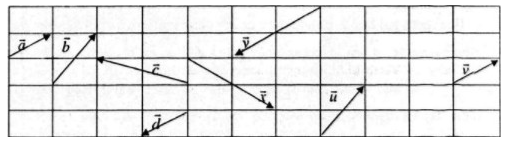
Trong hình 1.4, hãy chỉ ra các vec tơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.

Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi  \(\overrightarrow{AB}=\overrightarrow{DC}\).

Cho lục giác đều ABCDEF có tâm O.

a) Tìm các vec to khác \(\vec 0\) và cùng phương với \(\overrightarrow {OA}\)

b) Tìm các véc tơ bằng véc tơ \(\overrightarrow {AB}\)

Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vectơ  \(\overrightarrow{MA}+\overrightarrow{MB}\) và \(\overrightarrow{MA}-\overrightarrow{MB}\)

Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\) 

Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có 

a) \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0}\) 

b) \(\overrightarrow{AB}-\overrightarrow{AD}= \overrightarrow{CB}-\overrightarrow{CB}\) 

Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\)

Cho tam giác ABC cạnh a. Tính độ dài của các vectơ  \(\overrightarrow{AB}+\overrightarrow{BC}\)  và \(\overrightarrow{AB}-\overrightarrow{BC}\)

Cho hình bình hành ABCD  có tâm O. Chứng minh rằng:

a) \(\overrightarrow {CO}  - \overrightarrow {OB}  = \overrightarrow {BA} ;\)

b) \(\overrightarrow {AB}  - \overrightarrow {BC}  = \overrightarrow {DB} \)

c) \(\overrightarrow {DA}  - \overrightarrow {DB}  = \overrightarrow {OD}  - \overrightarrow {OC} \)

d) \(\overrightarrow {DA}  - \overrightarrow {DB}  + \overrightarrow {DC}  = \vec 0\)

Cho \(\overrightarrow{a}\), \(\overrightarrow{b}\) là hai vectơ khác\(\overrightarrow{0}\). Khi nào có đẳng thức

a) \(\left| {\vec a + \vec b} \right| = \left| {\vec a} \right| + \left| {\vec b} \right|;\)

b) \(\left| {\vec a + \vec b} \right|\,\, = \,\,\left| {\vec a - \vec b} \right|\)

Cho \(\left | \overrightarrow{a} +\overrightarrow{b}\right |= 0\) . So sánh độ dài, phương và hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\)

Chứng minh rằng \(\overrightarrow{AB}=\overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Cho ba lực \(\left | \overrightarrow{F_1} \right |=\overrightarrow{MA}, \left | \overrightarrow{F_2} \right |=\overrightarrow{MB}\) và\(\left | \overrightarrow{F_3} \right |=\overrightarrow{MC}\) cùng tác động vào một vât tại điểm M và đứng yên. Cho biết cường độ của \(\overrightarrow{F_1},\overrightarrow{F_2}\) đều là 100N và \(\widehat{AMB}=60^0\)

Tìm cường độ và hướng của lực\(\overrightarrow{F_3}\) .

Cho hình bình hành ABCD. Chứng mỉnh rằng:

 \(\overrightarrow{AB}\) \(+\) \(\overrightarrow{AC}\) \(+\) \(\overrightarrow{AD}\) \(=2\overrightarrow{AC}\).

Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ \( \overrightarrow{AB},\overrightarrow{BC},\overrightarrow{AC}\), theo hai vectơ sau \(\overrightarrow{u}=\overrightarrow{AK},\overrightarrow{v}=\overrightarrow{BM}\).

Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho \( \overrightarrow{MB}=3\overrightarrow{MC}\). Hãy phân tích vectơ  \(\overrightarrow{AM}\) theo hai vectơ  \(\overrightarrow{u}=\overrightarrow{AB}, \overrightarrow{v}=\overrightarrow{AC}\).

Gọi AM là trung tuyến của tam giác ABC  và D là trung điểm của đạn AM. Chứng minh rằng:

a) \(2\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{0}\)

b)  , với O là điểm tùy ý.

Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng: \(2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{BC}+\overrightarrow{AD}\)

Cho hai điểm phân biệt A và B. Tìm điểm K sao cho \(3\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}\).

Cho tam giác ABC. Tìm điểm m sao cho \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}\)

Cho tam giác đều ABC có trọng tâm O và M là một điểm tùy ý trong tam giác. Gọi D,E,F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng: \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF} =\frac{3}{2}\overrightarrow{MO}\)

Trên trục (O, ) cho các điểm A, B, M có tọa độ lần lượt là \(-1, 2, 3, -2\) .

a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục;

b) Tính độ dài đại số của \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\). Từ đó suy ra hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{MN}\) ngược hướng.

Trong mặt phẳng tọa độ các mệnh đề sau đúng hay sai?

a) \(\overrightarrow{a}= ( -3; 0)\)  và \(\overrightarrow{i}= (1; 0)\) là hai vectơ ngược hướng;

b) \(\overrightarrow{a}= ( 3; 4)\)  và \(\overrightarrow{i}= (-3; -4)\) là hai vectơ đối nhau;

c) \(\overrightarrow{a}= ( 5; 3)\)  và \(\overrightarrow{i}= (3; 5)\) là hai vectơ đối nhau;

d) hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau

Tìm tọa độ của các vec tơ sau:

a) \(\overrightarrow{a}=2\overrightarrow{j}\)                                  b) \(\overrightarrow{b}= -3\) 

c)  \(\overrightarrow{c}=3\overrightarrow{i} - 4\)                  d) \(\overrightarrow{d}= 0,2\) \(\overrightarrow{i} + \sqrt{3}\overrightarrow{j}\)

Trong mặt phẳng Oxy. Các khẳng định sau đúng hay sai?

a) Tọa độ của điểm A là tọa độ của vec tơ \(\overrightarrow{OA}\);

b) Điểm A nằm trên trục hoành thì có tung độ bằng 0;

c) Điểm A nằm trên trục tung thì có hoành độ bằng 0;

d) Hoành độ và tung độ của điểm A bằng nhau khi và chỉ khi A nằm trên tia phân giác của góc phần tư thứ nhất.

Trong các mặt phẳng Oxy cho điểm (x₀; y₀)

a) Tìm tọa độ điểm A đối xứng với M qua trục Ox;

b) Tìm tọa độ điểm B đối xứng với M qua trục Oy;

c) Tìm tọa độ điểm C đối xứng với M qua gốc O.

Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Tìm tọa độ điểm D.

Các điểm A'(-4; 1), B'(2;4), C(2, -2) lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC. Chứng minh trọng tâm của các tam giác ABC và A'B'C' trùng nhau.

Cho \(\overrightarrow{a}= (2; -2),\overrightarrow{b}= (1; 4)\). Hãy phân tích vectơ \(\overrightarrow{c} = (5; 0)\) theo hai vectơ  và 

Vectơ khác với đoạn thẳng như thế nào?

Các khẳng định sau có đúng không ?

a) Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.

b) Hai vectơ cùng phương với một vectơ thứ ba khác\(\overrightarrow 0 \) thì cùng phương.

c) Hai vectơ cùng hướng với một vectơ thứ ba thì cùng hướng.

d) Hai vectơ cùng hướng với một vectơ thứ ba khác \(\overrightarrow 0 \) thì cùng hướng.

e) Hai vectơ ngược hướng với một vectơ khác \(\overrightarrow 0 \) thì cùng hướng.

f) Điều kiện cần và đủ để hai vectơ bằng nhau là chúng có độ dài bằng nhau.

Trong hình 7 dưới đây, hãy chỉ ra các vectơ cùng phương, các vectơ cùng hướng và các vectơ bằng nhau.

Gọi C là trung điểm của đoạn thẳng AB. Các khẳng định sau đây đúng hay sai?

a) \(\overrightarrow {AC}\) và \(\overrightarrow {BC}\) cùng hướng.

b) \(\overrightarrow {AC}\) và \(\overrightarrow {AB}\) cùng hướng

c) \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\) ngược hướng

d) \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} }\right| \)

e) \(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BC} } \right|\)

f) \(\left| {\overrightarrow {AB} } \right| = 2\left| {\overrightarrow {BC} } \right|\)

Cho lục giác đều ABCDEF. Hãy vẽ các vectơ bằng vectơ \(\overrightarrow {AB}\) và ta có

a) Các điểm đầu là B, F, C.

b) Các điểm cuối là F, D, C.

Chứng minh rằng nếu \(\overrightarrow {AB}  = \overrightarrow {CD} \) thì \(\overrightarrow {AC}  = \overrightarrow {BD} \)

Tứ giác ABCDABCD là hình gì nếu \(\overrightarrow {AB}  = \overrightarrow {DC} \) và \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\)?

Cho bốn điểm bất kì M, N, P, Q. Chứng minh các đẳng thức sau:

\(\begin{array}{l}
a)\overrightarrow {PQ}  + \overrightarrow {NP}  + \overrightarrow {MN}  = \overrightarrow {MQ} \\
b)\overrightarrow {NP}  + \overrightarrow {MN}  = \overrightarrow {QP}  + \overrightarrow {MQ} \\
c)\overrightarrow {MN}  + \overrightarrow {PQ}  = \overrightarrow {MQ}  + \overrightarrow {PN} 
\end{array}\)

Các hệ thức sau đây đúng hay sai (với mọi \(\overrightarrow a\) và \(\overrightarrow b\)) ?

a) \(\left| {\overrightarrow a  + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b }\right| \)

b) \(\left| {\overrightarrow a  + \overrightarrow b } \right| \le \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)

Cho hình bình hành ABCDABCD với tâm O. Hãy điền vào chỗ trống (…) để được đẳng thức đúng

\(\begin{array}{l}
a)\overrightarrow {AB}  + \overrightarrow {AD}  = ...\\
b)\overrightarrow {AB}  + \overrightarrow {CD}  = ...\\
c)\overrightarrow {AB}  + \overrightarrow {OA}  = ...\\
d)\overrightarrow {OA}  + \overrightarrow {OC}  = ...\\
e)\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = ...
\end{array}\)

Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai ?

\(\begin{array}{l}
a)\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {BD} } \right|\\
b)\overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {BC} \\
c)\overrightarrow {OA}  + \overrightarrow {OB}  = \overrightarrow {OC}  + \overrightarrow {OD} \\
d)\overrightarrow {BD}  + \overrightarrow {AC}  = \overrightarrow {AD}  + \overrightarrow {BC} 
\end{array}\)

Cho tam giác đều ABC nội tiếp đường tròn tâm O.

a)  Hãy xác định các điểm M, N, P sao cho

\(\begin{array}{l}
\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} ;\\
\overrightarrow {ON}  = \overrightarrow {OB}  + \overrightarrow {OC} ;\\
\overrightarrow {OP}  = \overrightarrow {OC}  + \overrightarrow {OA} 
\end{array}\)

b) Chứng minh rằng \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \)

Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại O (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau

a) \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là 100N, góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 120⁰ (h.17a);

b) Cường độ của \(\overrightarrow {{F_1}} \) là 40N, của \(\overrightarrow {{F_2}} \) là 30N và góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng (h.17b).

Trả lời các câu hỏi sau đây:

a) Vectơ đối của vectơ \(-\overrightarrow a \) là vectơ nào?

b) Vectơ đối của vectơ  \(\overrightarrow 0 \) là vectơ nào?

c) Vectơ đối của vectơ \(\overrightarrow a  + \overrightarrow b \) là vectơ nào?

Chứng minh các mệnh đề sau đây:

a) Nếu \(\overrightarrow a  + \overrightarrow b  = \overrightarrow c \) thì 

\(\overrightarrow a  = \overrightarrow c  - \overrightarrow b ,\overrightarrow b  = \overrightarrow c  - \overrightarrow a \)

b) \(\overrightarrow a  - \left( {\overrightarrow b  + \overrightarrow c } \right) = \overrightarrow a  - \overrightarrow b  - \overrightarrow c \)

c) \(\overrightarrow a  - \left( {\overrightarrow b  - \overrightarrow c } \right) = \overrightarrow a  - \overrightarrow b  + \overrightarrow c \)

Cho hình bình hành ABCD với tâm O. Mỗi khẳng định sau đây đúng hay sai ?

a) \(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {AB} \)

b) \(\overrightarrow {CO}  - \overrightarrow {OB}  = \overrightarrow {BA} \)

c) \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {AC} \)

d) \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {BD} \)

e) \(\overrightarrow {CD}  - \overrightarrow {CO}  = \overrightarrow {BD}  - \overrightarrow {BO} \)

Cho hai điểm A, B phân biệt.

a) Tìm tập hợp các điểm O sao cho \(\overrightarrow {OA}  = \overrightarrow {OB} \);

b) Tìm tập hợp các điểm O sao cho \(\overrightarrow {OA}  =-\overrightarrow {OB} \) .

Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {DA}  - \overrightarrow {DB}  + \overrightarrow {DC}  = \overrightarrow 0 \).

Chứng minh rằng \(\overrightarrow {AB}  = \overrightarrow {CD} \) khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Cho sáu điểm A, B, C, D, E, F. Chứng minh rằng

\(\begin{array}{l}
\overrightarrow {AD}  + \overrightarrow {BE}  + \overrightarrow {CF} \\
 = \overrightarrow {AE}  + \overrightarrow {BF}  + \overrightarrow {CD} \\
 = \overrightarrow {AF}  + \overrightarrow {BD}  + \overrightarrow {CE} 
\end{array}\)

Cho tam giác ABCABC . Hãy xác định các vec tơ:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {AB}  + \overrightarrow {BC} ;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \overrightarrow {CB}  + \overrightarrow {BA} ;{\mkern 1mu} {\mkern 1mu} \\
\overrightarrow {AB}  + \overrightarrow {CA} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA}  + \overrightarrow {CB} ;
\end{array}\\
\begin{array}{l}
\overrightarrow {BA}  + \overrightarrow {CA} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {CB}  - \overrightarrow {CA} ;{\mkern 1mu} \\
\overrightarrow {AB}  - \overrightarrow {CB} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC}  - \overrightarrow {AB} .
\end{array}
\end{array}\)

Cho ba điểm O, A, B không thẳng hàng. Tìm điều kiện cần và đủ để vec tơ \(\overrightarrow {OA}  + \overrightarrow {OB} \) có giá là đường phân giác của góc AOB.

Gọi O là tâm của hình bình hành ABCD. Chứng minh rằng với điểm M bất kì, ta có

\(\overrightarrow {MO}  = \frac{1}{4}\left( {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right)\)

Cho tam giác ABC.

a) Tìm các điểm M và N sao cho

\(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \) và \(2\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0 \)

b) Với các điểm M, N ở câu a) , tìm các số p và q sao cho \(\overrightarrow {MN}  = p\overrightarrow {AB}  + q\overrightarrow {AC} \)

Cho đoạn thẳng AB và điểm I sao cho \(2\overrightarrow {IA}  + 3\overrightarrow {IB}  = \overrightarrow 0 \)

a) Tìm số k sao cho \(\overrightarrow {IA}  = k\overrightarrow {AB} \)

b) Chứng minh rằng với mọi điểm M ta có: \(\overrightarrow {MI}  = \frac{2}{5}\overrightarrow {MA}  + \frac{3}{5}\overrightarrow {MB} \)

Trong mặt phẳng tọa độ cho ba điểm A(- 1;3); B(4;2); C(3;5).

a) Chứng minh rằng ba điểm A. B, C không thẳng hàng.

b) Tìm tọa độ điểm D sao cho \(\overrightarrow {AD}  =  - 3\overrightarrow {BC} \).

c) Tìm tọa độ điểm E sao cho 0 là trọng tâm tam giác ABE.

Cho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vec tơ sau đây và tính độ dài của chúng

\(\begin{array}{l}
\overrightarrow {OA}  + \overrightarrow {OB} ;\\
\overrightarrow {OA}  - \overrightarrow {OB} ;\\
3\overrightarrow {OA}  + 4\overrightarrow {OB} ;\\
\frac{{21}}{4}\overrightarrow {OA}  + 2,5\overrightarrow {OB} ;\\
\frac{{11}}{4}\overrightarrow {OA}  - \frac{3}{7}\overrightarrow {OB} .
\end{array}\)

Cho tam giác OAB. Gọi M, N lần lượt là trung điểm hai cạnh OA và OB. Hãy tìm các số m và n thích hợp trong mỗi đẳng thức sau đây:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OM}  = m\overrightarrow {OA}  + n\overrightarrow {OB} \\
\overrightarrow {MN}  = m\overrightarrow {OA}  + n\overrightarrow {OB} 
\end{array}\\
\begin{array}{l}
\overrightarrow {AN}  = m\overrightarrow {OA}  + n\overrightarrow {OB} \\
\overrightarrow {MB}  = m\overrightarrow {OA}  + n\overrightarrow {OB.} 
\end{array}
\end{array}\)

Gọi M và N lần lượt là trung điểm các đoạn thẳng AB và CD. Chứng minh rằng:

\(2\overrightarrow {MN}  = \overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AD}  + \overrightarrow {BC} \)

Cho tam giác ABC và điểm G. Chứng minh rằng

a) Nếu \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \) thì G là trọng tâm tam giác ABC;

b) Nếu có điểm O sao cho \(\overrightarrow {OG}  = \frac{1}{3}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)\) thì G là trọng tâm tam giác ABC.

Gọi G là trọng tâm tam giác ABC. Đặt \(\overrightarrow a  = \overrightarrow {GA} \) và \(\overrightarrow b  = \overrightarrow {GB} \). Hãy biểu thị mỗi vec tơ \(\overrightarrow {AB} ,\overrightarrow {GC} ,\overrightarrow {BC} ,\overrightarrow {CA} \) qua các vec tơ \(\overrightarrow a\) và \(\overrightarrow b\)

Chứng minh rằng nếu G và G′ lần lượt là trọng tâm tam giác ABC và tam giác A′B′C′ thì

\(3\overrightarrow {GG'}  = \overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'} \)

Từ đó hãy suy ra điều kiện cần và đủ để hai tam giác ABC và A′B′C′ có trọng tâm trùng nhau.

Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.

Cho tứ giác ABCD. Chứng minh rằng:

a) Có một điểm G duy nhất sao cho \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \vec 0\). Điểm G như thế gọi là trọng tâm của bốn điểm A, B, C, D. Tuy nhiên, người ta vẫn quen gọi G là trọng tâm của từ giác ABCD.

b) Trọng tâm G là trung điểm của mỗi đoạn thẳng nối các trung điểm hai cạnh đối của tứ giác, nó cũng là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.

c) Trọng tâm G nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.

Trong mặt phẳng tọa độ, mỗi mệnh đề sau đúng hay sai ?

a) Hai vec tơ \(\overrightarrow a  = \left( {26;9} \right)\) và \(\overrightarrow b  = \left( {9;26} \right)\) bằng nhau.

b) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

c) Hai vec tơ đối nhau thì chúng có hoành độ đối nhau.

d) Vec tơ \(\overrightarrow a\) cùng phương với vec tơ \(\overrightarrow i\) nếu \(\overrightarrow a\) có hoành độ bằng 0.

e) Vec tơ \(\overrightarrow a\) có hoành độ bằng 0 thì nó cùng phương với vec tơ \(\overrightarrow j\).

Tìm tọa độ của các vectơ sau trong mặt phẳng tọa độ

\(\begin{array}{*{20}{l}}
{\vec a =  - \vec i;{\mkern 1mu} {\mkern 1mu} \vec b = 5\vec j;{\mkern 1mu} {\mkern 1mu} \vec c = 3\vec i - 4\vec j;}\\
\begin{array}{l}
\vec d = \frac{1}{2}\left( {\vec j - \vec i} \right);{\mkern 1mu} {\mkern 1mu} \vec e = 0,15\vec i + 1,3\vec j;\\
\vec f = \pi \vec i - \left( {\cos {{24}^0}} \right)\vec j
\end{array}
\end{array}\)

Cho \(\overrightarrow a  = \left( {2;1} \right),\,\,\overrightarrow b  = \left( {3;4} \right),\,\,\,\overrightarrow c  = \left( {7;2} \right)\).

a) Tìm tọa độ của vectơ \(\overrightarrow u  = 2\overrightarrow a  - 3\overrightarrow b  + \overrightarrow c \).

b) Tìm tọa độ của vec tơ \(\overrightarrow x\) sao cho \(\overrightarrow x  + \overrightarrow a  = \overrightarrow b  - \overrightarrow c \)

c) Tìm các số k,l để \(\overrightarrow c  = k\overrightarrow a  + l\overrightarrow b \)

Cho \(\overrightarrow u  = \frac{1}{2}\overrightarrow i  - 5\overrightarrow j ,\,\,\overrightarrow v  = k\overrightarrow i  - 4\overrightarrow j \).

Tìm các giá trị của k để hai vec tơ \(\overrightarrow u, \overrightarrow v\) cùng phương.

Trong các mệnh đề sau, mệnh đề nào đúng ?

a) Tọa độ của điểm A bằng tọa độ của vec tơ \(\overrightarrow {OA} \), với O là gốc tọa độ.

b) Hoành độ của một điểm bằng 0 thì điểm đó nằm trên trục hoành.

c) Điểm A nằm trên trục tung thì A có hoành độ bằng 0.

d) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ điểm P bằng trung bình cộng các hoành độ của hai điểm A và B

e) Tứ giác ABCD là hình bình hành khi và chỉ khi x_A+x_C = x_B+x_D và y_A+y_C = y_B+y_D.

Trong mặt phẳng tọa độ, cho ba điểm A(−3;4), B(1;1), C(9;−5).

a) Chứng minh ba điểm A, B, C thẳng hàng.

b) Tìm tọa độ điểm D sao cho A là trung điểm của BD.

c) Tìm tọa độ điểm E trên trục Ox sao cho A, B, E thẳng hàng.

Cho điểm M(x;y). Tìm tọa độ của các điểm

a) M₁ đối xứng với M qua trục Ox.

b) M₂ đối xứng với M qua trục Oy.

c) M₃ đối xứng với M qua gốc tọa độ O.

Trong mặt phẳng tọa độ, cho ba điểm A(−4;1), B(2;4), C(2;−2).

a) Tìm tọa độ của trọng tâm tam giác ABC.

b) Tìm tọa độ điểm D sao cho C là trọng tâm tam giác ABD.

c) Tìm tọa độ điểm E sao cho ABCE là hình bình hành.

Cho sáu điểm A, B, C, D, E, F. Đẳng thức nào dưới đây đúng ?

(A) \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {FA}  + \overrightarrow {BC}  + \overrightarrow {EF}  + \overrightarrow {DE}  = \vec 0\)

(B) \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {FA}  + \overrightarrow {BC}  + \overrightarrow {EF}  + \overrightarrow {DE}  = \overrightarrow {AF} \)

(C) \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {FA}  + \overrightarrow {BC}  + \overrightarrow {EF}  + \overrightarrow {DE}  = \overrightarrow {AE} \)

(D) \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {FA}  + \overrightarrow {BC}  + \overrightarrow {EF}  + \overrightarrow {DE}  = \overrightarrow {AD} \)

Cho hình thang ABCD với hai cạnh đáy là AB = 3a và CD = 6a. Khi đó \(\left| {\overrightarrow {AB}  + \overrightarrow {CD} } \right|\) bằng bao nhiêu ?

(A) 9a$\mathrm{}$

(B) 3a

(C) −3a$$

(D) 0

Cho hình vuông ABCD có cạnh bằng a. Khi đó giá trị \(\left| {\overrightarrow {AC}  + \overrightarrow {BD} } \right|\) bằng bao nhiêu ?

(A) \(2a\sqrt 2 \)

(B) 2a

(C) a$$

(D) 0

Cho ba điểm bất kì A, B, C. Đẳng thức nào dưới đây đúng ?

(A) \(\overrightarrow {AB}  = \overrightarrow {CB}  - \overrightarrow {CA} \) 

(B) \(\overrightarrow {BC}  = \overrightarrow {AB}  - \overrightarrow {AC} \)

(C) \(\overrightarrow {AC}  - \overrightarrow {CB}  = \overrightarrow {BA} \)  

​(D) \(\overrightarrow {CA}  - \overrightarrow {CB}  = \overrightarrow {AB} \)     

Cho tam giác đều ABC có cạnh bằng a. Giá trị \(\left| {\overrightarrow {AB}  - \overrightarrow {CA} } \right|\) bằng bao nhiêu ?

(A) 2a

(B) a

(C) \(a\sqrt 3 \)

(D) \(\frac{{a\sqrt 3 }}{2}\)

Cho hai tam giác ABC và A′B′C′ lần lượt có trọng tâm là G và G′. Đẳng thức nào dưới  đây là sai ?

(A) \(3\overrightarrow {GG'}  = \overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'} \)                    

(B) \(3\overrightarrow {GG'}  = \overrightarrow {AB'}  + \overrightarrow {BC'}  + \overrightarrow {CA'} \)

(C) \(3\overrightarrow {GG'}  = \overrightarrow {AC'}  + \overrightarrow {BA'}  + \overrightarrow {CB'} \)                        

(D) \(3\overrightarrow {GG'}  = \overrightarrow {A'A}  + \overrightarrow {BB'}  + \overrightarrow {CC'} \)

Cho điểm B nằm giữa hai điểm A và C, với \(AB = 2a,AC = 6a\). Đẳng thức nào dưới đây đúng ?

(A) \(\overrightarrow {BC}  = \overrightarrow {AB} \)                                   

(B) \(\overrightarrow {BC}  =  - 2\overrightarrow {AB} \)

(C) \(\overrightarrow {BC}  = 4\overrightarrow {AB} \)                                               

(D) \(\overrightarrow {BC}  =  - 2\overrightarrow {BA} \)

Cho ba điểm phân biệt A, B, C. Nếu \(\overrightarrow {AB}  =  - 3\overrightarrow {AC} \) thì đẳng thức nào dưới đây đúng ?

(A) \(\overrightarrow {BC}  = 4\overrightarrow {AC} \)                                               

(B) \(\overrightarrow {BC}  =  - 4\overrightarrow {AC} \)

(C) \(\overrightarrow {BC}  = 2\overrightarrow {AC} \)                                           

(D) \(\overrightarrow {BC}  =  - 2\overrightarrow {AC} \)

Điều kiện nào dưới đây là cần và đủ để điểm O là trung điểm của đoạn thẳng AB?

(A) OA = OB                                                

(B) \(\overrightarrow {OA}  = \overrightarrow {OB} \)

(C) \(\overrightarrow {AO}  = \overrightarrow {BO} \)                                           

(D) \(\overrightarrow {OA}  + \overrightarrow {OB}  = \vec 0.\)

Nếu G là trọng tâm tam giác ABC thì đẳng thức nào dưới đây đúng ?

(A) \(\overrightarrow {AG}  = \frac{{\overrightarrow {AB}  + \overrightarrow {AC} }}{2}\)                              

(B) \(\overrightarrow {AG}  = \frac{{\overrightarrow {AB}  + \overrightarrow {AC} }}{3}\)

(C) \(\overrightarrow {AG}  = \frac{{3\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)}}{2}\)                                 

(D) \(\overrightarrow {AG}  = \frac{{2\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)}}{3}\)

Gọi AM là trung tuyến của tam giác ABC, và I là trung điểm của AM. Đẳng thức nào sau đây là đúng ?

(A) \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \vec 0\)

(B) \( - \overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \vec 0\)

(C) \(\overrightarrow {IA}  + \overrightarrow {IB}  - \overrightarrow {IC}  = \vec 0\)     

(D) \(2\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \vec 0\)

Trong mặt phẳng tọa độ Oxy cho hai điểm A(−1;4), B(3;−5). Khi đó tọa độ của vectơ \(\overrightarrow {BA} \) là cặp số nào ?

(A) (2;−1)$$

(B) (−4;9)

(C) (4;−9)$$

(D) (4;9)

Trong mặt phẳng tọa độ Oxy cho hai điểm A(0;5), B(2;−7). Khi đó tọa độ trung điểm của đoạn thẳng AB là cặp số nào ?

(A) (2;−2)

(B) (−2;12)

(C) (−1;6)

(D) (1;−1)

Trong mặt phẳng tọa độ Oxy cho hai điểm M(8;−1), N(3;2). Nếu P là điểm đối xứng với điểm M qua điểm N thì tọa độ của P là cặp số nào ?

(A) (−2;5)$$

(B) \(\left( {\frac{{11}}{2};\frac{1}{2}} \right)\)

(C) (13;−3)$$

(D) (11;−1)

Trong mặt phẳng tọa độ Oxy cho ba điểm A(5;−2), B(0;3), C(−5;−1). Khi đó trọng tâm tam giác ABC có tọa độ là cặp số nào ?

(A) (1;−1)

(B) (0;0)

(C) (0;11)

(D) (10;0)

Trong mặt phẳng tọa độ Oxy cho tam giác ABC với trọng tâm G. Biết rằng A(−1;4), B(2;5), G(0;7). Hỏi tọa đô đỉnh C là cặp số nào ?

(A) (2;12)$$

(B) (−1;12)

(C) (3;1)

(D) (1;12)

Trong mặt phẳng tọa độ Oxy cho bốn điểm A(3;1), B(2;2), C(1;6), D(1;−6). Hỏi điểm G(2;−1) là trọng tâm của tam giác nào sau đây ?

(A) Tam giác ABC$$

(B) Tam giác ABD

(C) Tam giác ACD

(D) Tam giác BCD