Bài tập 3 trang 7 SGK Hình học 10

Bài tập 3 trang 7 SGK Hình học 10

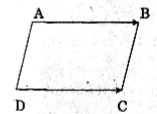
Giả sử tứ giác ABCD là hình bình hành.

Khi đó \(AB = DC \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {DC} } \right|.\)

Mặt khác, dễ thấy \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) cùng hướng.

Từ đấy, suy ra \(\overrightarrow {AB}  = \overrightarrow {DC} \)

Ngược lại, giả sử tứ giác ABCD có \(\overrightarrow {AB}  = \overrightarrow {DC} \), đều này chứng tỏ:

\(\overrightarrow {AB}  = \overrightarrow {DC} \)và AB // CD

Hay AB = CD và AB // CD

Nên tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).

-- Mod Toán 10