Bài tập 4 trang 7 SGK Hình học 10

Bài tập 4 trang 7 SGK Hình học 10

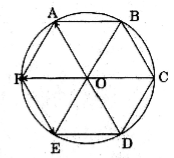
Tâm O của lục giác đều chính là tâm đường tròn đi qua sáu điểm A, B, C, D, E, F. Vì ABCDEF là lục giác đều nên các tứ giác ABCO, BCDO, CDEO, DEFO, EFAO, FABO là các hình thoi bằng nhau.

Câu a:

Ta thấy giá của các vecto: \(\overrightarrow {CD} ,\overrightarrow {DO} ,\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {DA} ,\overrightarrow {{\rm{EF}}} ,\overrightarrow {FE} ,\overrightarrow {{\rm{BC}}} ,\overrightarrow {{\rm{CB}}} \) song song hoặc trùng với giá của vecto \(\overrightarrow {OA} \), do vậy chín vecto trên cùng phương với vecto \(\overrightarrow {OA} \).

Câu b:

Do các tứ giác nói trên là những hình thoi bằng nhau nên:

 \[\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {FO} } \right| = \left| {\overrightarrow {OC} } \right| = \left| {\overrightarrow {ED} } \right|\,\,\,\,\,\,(1)\]

Mặt khác dễ thấy rằng các vecto \(\overrightarrow {AB} ,\overrightarrow {FO} ,\overrightarrow {\,\,OC} ,\,\,\,\overrightarrow {ED} \) là cùng hướng (2)

Từ (1) và (2) ta có những vecto bằng vecto \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {\,\,OC} ,\,\,\,\overrightarrow {ED} .\)

-- Mod Toán 10