Bài tập 11 trang 14 SGK Hình học 10 NC

Bài tập 11 trang 14 SGK Hình học 10 NC

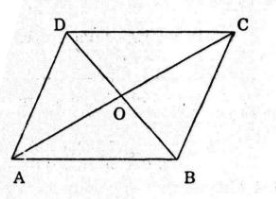
a) Sai vì \(\left| {\overrightarrow {AB}  + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| \ne \left| {\overrightarrow {BD} } \right|\)

b) Đúng vì \(\overrightarrow {AB}  + \overrightarrow {BD}  = \overrightarrow {AD}  = \overrightarrow {BC} \)

c) Sai. Vì

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OA}  + \overrightarrow {OB} \\
 = \left( {\overrightarrow {OC}  + \overrightarrow {CA} } \right) + \left( {\overrightarrow {OD}  + \overrightarrow {DB} } \right)
\end{array}\\
\begin{array}{l}
 = \left( {\overrightarrow {OC}  + \overrightarrow {OD} } \right) + \left( {\overrightarrow {CA}  + \overrightarrow {DB} } \right)\\
 \ne \overrightarrow {OC}  + \overrightarrow {OD} 
\end{array}
\end{array}\)

d) Đúng. Vì 

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {BD}  + \overrightarrow {AC} \\
 = \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) + \left( {\overrightarrow {AD}  + \overrightarrow {DC} } \right)
\end{array}\\
\begin{array}{l}
 = \left( {\overrightarrow {DC}  + \overrightarrow {CD} } \right) + \left( {\overrightarrow {BC}  + \overrightarrow {AD} } \right)\\
 = \overrightarrow {AD}  + \overrightarrow {BC} 
\end{array}
\end{array}\)

-- Mod Toán 10