Bài tập 8 trang 36 SGK Hình học10 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 8 trang 36 SGK Hình học10 NC
Cho hình thang ABCD với hai cạnh đáy là AB = 3a và CD = 6a. Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right|\) bằng bao nhiêu ?
(A) 9a
(B) 3a
(C) −3a
(D) 0
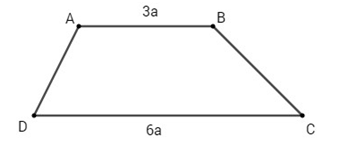
Gọi E là trung điểm CD. Ta có:
\(\begin{array}{l}
\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {DE} + \overrightarrow {CD} } \right|\\
= \left| {\overrightarrow {CE} } \right| = CE = 3a
\end{array}\)
Chọn (B).
-- Mod Toán 10
Copyright © 2021 HOCTAP247
