Bài tập 4 trang 12 SGK Hình học 10

Bài tập 4 trang 12 SGK Hình học 10

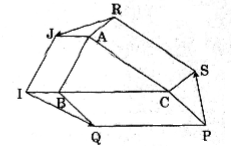
Vì tứ giác ABIJ là hình bình hành, nên \(\overrightarrow {IB}  = \overrightarrow {JA} \) , do vậy \(\overrightarrow {IQ}  = \overrightarrow {IB}  + \overrightarrow {BQ} \) hay \(\overrightarrow {IQ}  = \overrightarrow {JA}  + \overrightarrow {BQ} \,\,(1)\)

Vì tứ giác BCPQ là hình bình hành, nên \(\overrightarrow {PC}  = \overrightarrow {QB} \) do vậy \(\overrightarrow {PS}  = \overrightarrow {PC}  + \overrightarrow {CS} \,\,hay\,\,\overrightarrow {PS}  = \overrightarrow {QB}  + \overrightarrow {{\rm{AR}}} \,\,(2)\) (vì \(\overrightarrow {AR}  = \overrightarrow {CS} \))

Ta cũng có \(\overrightarrow {RJ}  = \overrightarrow {RA}  + \overrightarrow {{\rm{AJ}}} \,\,(3)\)

Từ các đẳng thức (1),(2), (3), ta có:

\(\overrightarrow {RJ}  + \overrightarrow {IQ}  + \overrightarrow {PS}  = \overrightarrow {RA}  + \overrightarrow {AJ}  + \overrightarrow {JA}  + \overrightarrow {BQ}  + \overrightarrow {QB}  + \overrightarrow {AR} \)

\( = \overrightarrow {RA}  + \overrightarrow {AA}  + \overrightarrow {BB}  + \overrightarrow {AR} \)

\(\begin{array}{l} = \overrightarrow {RA}  + \vec 0 + \vec 0 + \overrightarrow {AR} \\ = \overrightarrow {RA}  + \overrightarrow {AR}  = \overrightarrow {RR}  = \vec 0\end{array}\)

-- Mod Toán 10