Bài tập 27 trang 24 SGK Hình học 10 NC
Bài tập 27 trang 24 SGK Hình học 10 NC
Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.
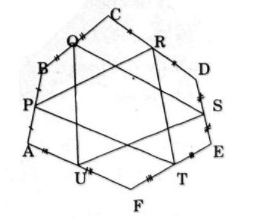
Lấy O bất kì và gọi K, G lần lượt là trọng tâm tam giác PRT và QSU, ta có:
\(\begin{array}{l}
3\overrightarrow {OG} = \overrightarrow {OP} + \overrightarrow {OR} + \overrightarrow {OT} \\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \frac{1}{2}\left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + \frac{1}{2}\left( {\overrightarrow {OE} + \overrightarrow {OF} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\\
3\overrightarrow {OK} = \overrightarrow {OQ} + \overrightarrow {OS} + \overrightarrow {OU} \\
= \frac{1}{2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right) + \frac{1}{2}\left( {\overrightarrow {OD} + \overrightarrow {OE} } \right) + \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OF} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)
\end{array}\)
Từ (1) và (2) suy ra \(\overrightarrow {OG} = \overrightarrow {OK} \) hay G ≡ K
Vậy hai tam giác PRT và QSU có trọng tâm trùng nhau.
-- Mod Toán 10
Copyright © 2021 HOCTAP247
