Bài tập 2 trang 12 SGK Hình học 10
Bài tập 2 trang 12 SGK Hình học 10
Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\)
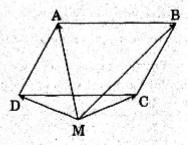
Do đẳng thức (1) nên ta có:
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MC} + ( - \overrightarrow {MC} - \overrightarrow {MB} )\\ = \overrightarrow {MB} + \overrightarrow {MD} + ( - \overrightarrow {MC} - \overrightarrow {MB} )\\ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MC} + ( - \overrightarrow {MC} ) + ( - \overrightarrow {MB} )\\ = \overrightarrow {MB} + \overrightarrow {MD} - \overrightarrow {MC} - \overrightarrow {MB} \\ \Leftrightarrow \overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {MD} - \overrightarrow {MC} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CD} .\end{array}\)
Vì ABCD là hình bình hành nên \(\overrightarrow {BA} = \overrightarrow {CD} \), do vậy (1) là đẳng thức đúng.
-- Mod Toán 10
Copyright © 2021 HOCTAP247
