Bài tập 3 trang 17 SGK Hình học 10
Bài tập 3 trang 17 SGK Hình học 10
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho \( \overrightarrow{MB}=3\overrightarrow{MC}\). Hãy phân tích vectơ \(\overrightarrow{AM}\) theo hai vectơ \(\overrightarrow{u}=\overrightarrow{AB}, \overrightarrow{v}=\overrightarrow{AC}\).
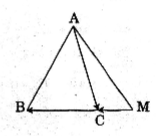
Ta có: \(\overrightarrow {AM} = \overrightarrow {AC} + \overrightarrow {CM} \,\,\,\,\,\,\,\,\,(1)\)
Vì \(\overrightarrow {CM} \) cùng hướng với \(\overrightarrow {BC} ,\) hơn nữa \(\left| {\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {CM} } \right|,\) nên
\(\overrightarrow {CM} = \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}(\overrightarrow {AC} - \overrightarrow {AB} )\,\,\,\,\,\,(2)\)
Từ (1) và (2) ta có:
\(\overrightarrow {AM} = \overrightarrow {AC} + \frac{1}{2}(\overrightarrow {AC} - \overrightarrow {AB} ) \Leftrightarrow \overrightarrow {AM} = \frac{3}{2}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} .\)
Vậy \(\overrightarrow {AM} = \frac{3}{2}\vec v - \frac{1}{2}\vec u.\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
