Bài tập 2 trang 17 SGK Hình học 10

Bài tập 2 trang 17 SGK Hình học 10

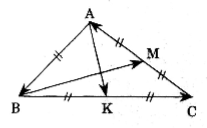
Do tính chất trung điểm nên từ giả thiết ta có:

\(\left\{ \begin{array}{l}2\overrightarrow {AK}  = \overrightarrow {AB}  + \overrightarrow {AC} \\2\overrightarrow {BM}  = \overrightarrow {BA}  + \overrightarrow {BC} \end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AB}  - \overrightarrow {CA}  = 2\vec u\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\ - \overrightarrow {AB}  + \overrightarrow {BC}  = 2\vec v\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)

Mặt khác, ta có: \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = \overrightarrow {AC}  + \overrightarrow {CA} \)

\( \Leftrightarrow \,\,\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = \vec 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)\)

Từ (1) và (2) ta có:

\((\overrightarrow {AB}  - \overrightarrow {CA} ) + ( - \overrightarrow {AB}  + \overrightarrow {BC} ) = 2\vec u + 2\vec v\)

\( \Leftrightarrow \overrightarrow {AB}  - \overrightarrow {CA}  - \overrightarrow {AB}  + \overrightarrow {BC}  = 2\vec u + 2\vec v\)

\( \Leftrightarrow  - \overrightarrow {CA}  + \overrightarrow {BC}  = 2\vec u + 2\vec v\) (4)

Từ (2) và (3) ta có:

\( - \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec v\)

\( \Leftrightarrow 2\overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5)\)

Từ (4) và (5) suy ra:

\( - \overrightarrow {AB}  + \overrightarrow {BC}  + 2\overrightarrow {BC}  + \overrightarrow {CA}  = 2\vec u + 2\vec v + 2\vec v\)

\( \Leftrightarrow 3\overrightarrow {BC}  = 2\vec u + 4\vec v \Leftrightarrow \overrightarrow {BC}  = \frac{2}{3}\vec u + \frac{4}{3}\vec v\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(6)\)

Từ (5) và (6) ta có:

\(\frac{4}{3}\vec u + \frac{8}{3}\vec v\, + \overrightarrow {CA}  = 2\vec v \Rightarrow \overrightarrow {CA}  =  - \frac{4}{3}\vec u + \frac{2}{3}\vec v\,\,\,\,\,\,\,\,\,(7)\)

Từ (7) và (1), ta có được:

\(\overrightarrow {AB}  + \frac{4}{3}\vec u + \frac{2}{3}\vec v = 2\vec u \Leftrightarrow \overrightarrow {AB}  = \frac{2}{3}\vec u - \frac{2}{3}\vec v\)

Kết luận:

\(\overrightarrow {AB}  = \frac{2}{3}\vec u - \frac{2}{3}\vec v\)

\(\overrightarrow {BC}  = \frac{2}{3}\vec u + \frac{4}{3}\vec v\)

\(\overrightarrow {CA}  =  - \frac{4}{3}\vec u - \frac{2}{3}\vec v\)

-- Mod Toán 10