Bài tập 1 trang 7 SGK Hình học 10
Bài tập 1 trang 7 SGK Hình học 10
Cho ba vectơ \(\vec a,\vec b,\vec c\) đều khác vec tơ \(\vec 0\). Các khẳng định sau đây đúng hay sai?
a) Nếu hai vectơ \(\vec a,\vec b\) cùng phương với \(\vec c\) thì \(\vec a,\vec b\) cùng phương.
b) Nếu \(\vec a,\vec b\) cùng ngược hướng với \(\vec c\) thì \(\vec a\) và \(\vec b\) cùng hướng .
Câu a:
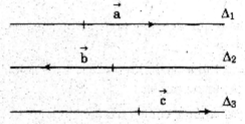
Ta gọi \({\Delta _1},{\Delta _2},{\Delta _3}\) lần lượt là giá của \(\overrightarrow a ,\overrightarrow b \) và \(\overrightarrow c \). Vì \(\overrightarrow a ,\overrightarrow b \)cùng phương với \(\overrightarrow c \) nên \({\Delta _1}\) song song hoặc trùng \({\Delta _3}\) và \({\Delta _2}\) song song hoặc trùng \({\Delta _3}\), từ đấy suy ra \({\Delta _1}\)song song hoặc trùng \({\Delta _2}\), tức là \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương.
Vậy khẳng định đã cho là đúng.
Câu b:
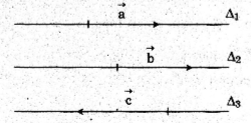
Nếu \(\overrightarrow a \) ngược hướng với \(\overrightarrow b \) thì \(\overrightarrow b \) và \(\overrightarrow c \) cùng hướng, ta có mâu thuẫn
Vậy \(\overrightarrow a \) và \(\overrightarrow b \)cùng hướng.
-- Mod Toán 10
Copyright © 2021 HOCTAP247
