Bài tập 21 trang 23 SGK Hình học 10 NC
Bài tập 21 trang 23 SGK Hình học 10 NC
Cho tam giác vuông cân OAB với OA = OB = a. Hãy dựng các vec tơ sau đây và tính độ dài của chúng
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} ;\\
\overrightarrow {OA} - \overrightarrow {OB} ;\\
3\overrightarrow {OA} + 4\overrightarrow {OB} ;\\
\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} ;\\
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} .
\end{array}\)
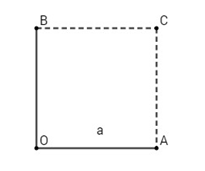
Vẽ hình vuông OACB, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \\
\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = a\sqrt 2
\end{array}\\
\begin{array}{l}
\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \\
\Rightarrow \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right| = \left| {\overrightarrow {BA} } \right| = a\sqrt 2
\end{array}
\end{array}\)
Gọi M, N là điểm thỏa mãn:
\(\overrightarrow {OM} = 3\overrightarrow {OA} ,\overrightarrow {ON} = 4\overrightarrow {OB} \)
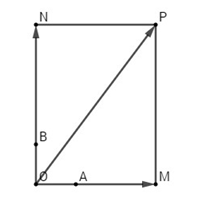
Vẽ hình chữ nhật MONP, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\overrightarrow {OM} + \overrightarrow {ON} = {\mkern 1mu} \overrightarrow {OP} \\
\Rightarrow \left| {\overrightarrow {OM} + \overrightarrow {ON} } \right| = \left| {\overrightarrow {OP} } \right|\\
= \sqrt {O{M^2} + O{N^2}}
\end{array}\\
{ = \sqrt {9{a^2} + 16{a^2}} = 5a}
\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}
\left| {\frac{{21}}{4}\overrightarrow {OA} + 2,5\overrightarrow {OB} } \right|\\
= \sqrt {{{\left( {\frac{{21}}{4}a} \right)}^2} + {{\left( {\frac{5}{2}a} \right)}^2}} \\
= \frac{{\sqrt {241} }}{4}a
\end{array}\)
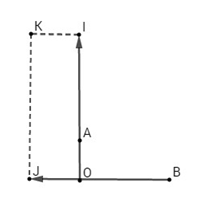
Gọi I, J là điểm thỏa mãn:
\(\overrightarrow {OI} = \frac{{11}}{4}\overrightarrow {OA} ;\overrightarrow {OJ} = - \frac{3}{7}\overrightarrow {OB} \)
Vẽ hình chữ nhật OIKJ, ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} = \frac{{11}}{4}\overrightarrow {OA} + \left( { - \frac{3}{7}} \right)\overrightarrow {OB} \\
= \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow {OK}
\end{array}\\
\begin{array}{l}
\Rightarrow \left| {\frac{{11}}{4}\overrightarrow {OA} - \frac{3}{7}\overrightarrow {OB} } \right| = \left| {\overrightarrow {OK} } \right|\\
= \sqrt {{{\left( {\frac{{11}}{4}a} \right)}^2} + {{\left( { - \frac{3}{7}a} \right)}^2}} = \frac{{\sqrt {6073} }}{{28}}a
\end{array}
\end{array}\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
