Bài tập 10 trang 12 SGK Hình học 10

Bài tập 10 trang 12 SGK Hình học 10

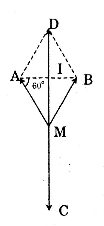
Do ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng tác động vào vật mà vật đứng yên nên tổng hợp lực phải bằng vecto không tức là

\(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \vec 0\)

\( \Leftrightarrow \overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = \vec 0\,\,\,\,(*)\)

Dựng hình bình hành AMBD, ta có:

\((*) \Leftrightarrow \overrightarrow {MD}  + \overrightarrow {MC}  = \vec 0\)

\( \Leftrightarrow \) M là trung điểm của DC như vậy hướng của lực \(\overrightarrow {{F_3}} \) ngược với hướng của tổng hợp lực \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} .\) Ta tính cường độ của lực \(\overrightarrow {{F_3}} \) ta có:

\(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MD} } \right| = 2MI\)

\( = 2.\frac{{100.\sqrt 3 }}{2} = 100\sqrt 3 (N).\)

-- Mod Toán 10