Bài tập 7 trang 77 SGK SGK Đại số & Giải tích 11

Bài tập 7 trang 77 SGK SGK Đại số & Giải tích 11

Không gian mẫu gồm 216 phần tử có dạng:

\(\Omega =\left \{ (i,j,k) \setminus i,j,k \in \mathbb{Z},1\leq i,j,k\leq 6 \right \}\)

Đặt 

\(A=\left \{ (6,i,j) \setminus 1\leq i,j,\leq 6 \right \}\)

\(B=\left \{ (i,6,j) \setminus 1\leq i,j,\leq 6 \right \}\)

\(C=\left \{ (i,j,6) \setminus 1\leq i,j,\leq 6 \right \}\)

Gọi biến cố có ít nhất một mặt 6 chấm xuất hiện là D.

Ta có \(D=A\cup B\cup C, n(A)=36, n(B)=36,n(C)=36\)

Mặt khác \(A\cap B=\left \{ (6,6,1);(6,6,2);(6,6,3);(6,6,4);(6,6,5);(6,6,6) \right \}\)

\(B\cap C=\left \{ (1, 6,6);(2,6,6);(3,6,6);(4,6,6);(5,6,6);(6,6,6) \right \}\)

\(C\cap A=\left \{ (6,1,6);(6,2,6);(6,3,6);(6,4,6);(6,5,6);(6,6,6) \right \}\)

\(A\cap B\cap C=\left \{ (6,6,6) \right \}\)

Dùng sơ đồ Ven ta có sự biểu diễn sau:

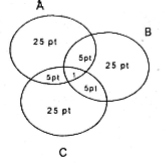
Từ sơ đồ này ta có: \(n(D)=n(A\cup B\cup C)=91\) (phần tử)

Do đó xác suất của biến cố có ít nhất mặt 6 chấm xuất hiện là: \(P(D)=\frac{91}{216}\)

-- Mod Toán 11