Chương 1: Hàm Số Lượng Giác Và Phương Trình Lượng Giác

Hãy xác định các giá trị của x trên đoạn  \(\small \left [- \pi ;\frac{3 \pi }{2} \right ]\) để hàm số \(\small y = tanx\);

a) Nhận giá trị bằng 0

b) Nhận giá trị bằng 1  

c) Nhận giá trị dương 

d) Nhận giá trị âm.  

Tìm tập xác định của các hàm số:

a) \(\small y=\frac{1+cosx}{sinx}\) ;

b)  \(\small y=\sqrt{\frac{1+cosx}{1-cosx}}\) ;

c)  \(\small y=tan(x-\frac{\pi }{3})\) ;

d)  \(\small y=cot(x+\frac{\pi }{6})\) .

Dựa vào đồ thị hàm số \(\small y = sinx\), hãy vẽ đồ thị của hàm số \(\small y = |sinx|\).

Chứng minh rằng \(\small sin2(x + k \pi ) = sin 2x\) với mọi số nguyên k. Từ đó vẽ đồ thị hàm số \(\small y = sin2x\).

Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của x để cosx =  .

Dựa vào đồ thị hàm số y = sinx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.

Dựa vào đồ thị hàm số y = cos x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm.

Giải các phương trình sau:

a)  \(\small sin (x + 2) =\frac{1}{3}\) 

b) \(\small sin 3x = 1\) 

c) \(\small sin (\frac{2x}{3} -\frac{\pi}{3}) =0\)

d) \(\small sin (2x + 20^0) =-\frac{\sqrt{3}}{2}\) 

Với những giá trị nào của x thì giá trị của các hàm số y = sin3x và y = sin x bằng nhau?

Giải các phương trình sau:

a) \(\small cos (x - 1) =\frac{2}{3}\)                      

b) \(\small cos 3x = cos 12^0\) 

c)  \(\small cos (\frac{3x}{2}-\frac{\pi}{4})=-\frac{1}{2}\)                

d)  .

Với những giá trị nào của x thì giá trị của các hàm số \(\small y = tan ( \frac{\pi}{4}- x)\) và \(\small y = tan2x\)  bằng nhau?

Giải các phương trình sau:

a) \(sin 3x - cos 5x = 0\);

b) \(\small tan 3x . tan x = 1\).

Giải phương trình: \(\small sin^2x - sinx = 0\)

Giải các phương trình sau:

a) \(\small 2cos^2x - 3cosx + 1 = 0\);

b) \(\small 2sin2x + \sqrt{2}sin4x = 0\).

Giải các phương trình sau:

a) \(sin^2(\frac{x}{2}) - 2cos(\frac{x}{2}) + 2 = 0\);          

b) \(\small 8cos^2x + 2sinx - 7 = 0\);

c) \(\small 2tan^2x + 3tanx + 1 = 0\);              

 d) \(\small tanx -2cotx + 1 = 0\).

Giải các phương trình sau:

a) \(\small 2sin^ 2x + sinxcosx - 3cos^2x = 0\)

b) \(\small 3sin^2x - 4sinxcosx + 5cos^2x = 2\)

c) \(\small 3sin^2x - sin2x + 2cos^2x = \frac{1}{2}\)

d) \(\small 2cos^2x -3\sqrt{3}sin2x -4sin^2x = -4\)

Giải các phương trình sau:

a) \(\small cosx - \sqrt{3}sinx = \sqrt{2}\)

b) \(\small 3sin3x - 4cos3x = 5\)

c) \(\small 2sin2x + 2cos2x -\sqrt{2} = 0\)

d) \(\small 5cos2x + 12sin2x - 13 = 0\) 

Giải phương trình:

a. \(\small tan(2x + 1) tan(3x - 1) = 1\)

b. \(\small tanx + tan(x + \frac{\pi }{4}) = 1\)

Tìm giá trị lớn nhất của hàm số:

a) \(y=2\sqrt{cosx}+1\)

b) \(y=3-2sinx.\)

a) Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?

b) Hàm số \(y=tan\left ( x+\frac{\pi }{5} \right )\) có phải là hàm số lẻ không? Tại sao?

Căn cứ vào đồ thị hàm số y = sin x, tìm các giá trị của x trên đoạn \(\left [ -\frac{3\pi }{2};2\pi \right ]\) để hàm số đó:

a) Nhận giá trị bằng -1.

b) Nhận giá trị âm.

Tìm giá trị lớn nhất của các hàm số:

a) \(y=\sqrt{2(1+cosx)}+1\)

b) \(y=3sin(x-\frac{\pi }{6})-2\)

Giải các phương trình sau:

a) \(sin(x+1)=\frac{2}{3}\)

b) \(sin^22x=\frac{1}{2}\)

c) \(cot^2 \frac{x}{2}=\frac{1}{3}\)

d) \(tan \left ( \frac{x}{12} +12x \right )=-\sqrt{3}\)​

Giải các phương trình sau:

a) 2cos²x – 3cosx + 1 = 0

b) 25sin²x + 15sin2x + 9 cos²x = 25

c) 2 sin x + cosx = 1

d) sinx + 1,5 cotx = 0

Phương trình cosx = sin x có số nghiệm thuộc đoạn [\(-\pi;\pi\)]

(A). 2                   (B). 4                 (C). 5                   (D). 6

Phương trình \(\frac{cos4x}{cos2x}=tan2x\) có số nghiệm thuộc khoảng \(\left ( 0;\frac{\pi}{2} \right )\) là:

A. 2                  B. 3                            C. 4                                 D .5

Nghiệm dương nhỏ nhất của phương trình 2tan²x + 5tanx + 3 = 0 là:

A. \(-\frac{\pi }{3}\)           B. \(-\frac{\pi }{4}\)                   C. \(-\frac{\pi }{6}\)                      D. \(-\frac{5\pi }{6}\)

Nghiệm dương nhỏ nhất của phương trình sin x + sin²x = cosx + 2 cos² x là:

A.\(\frac{\pi }{6}\)           B.\(\frac{2\pi }{3}\)                   C. \(\frac{\pi }{4}\)                   D. \(\frac{\pi }{3}\)

Phương trình 2tanx – 2 cotx – 3 = 0 có số nghiệm thuộc khoảng \(\left ( -\frac{\pi }{2}; \pi \right )\) là:

A. 1        B. 2            C. 3            D. 4

Tìm tập xác định của mỗi hàm số sau :

a. \(y = \sqrt {3 - \sin x} \);                                                                

b. \(y = \frac{{1 - \cos x}}{{\sin x}}\)

c. \(y = \sqrt {\frac{{1 - \sin x}}{{1 + \cos x}}} \)                                                             

d. \(y = \tan \left( {2x + \frac{\pi }{3}} \right)\)

Xét tính chẵn – lẻ của hàm số sau :

a. y = −2sinx

b. y = 3sinx–2

c. y = sinx–cosx

d. y = sinxcos²x+tanx

Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:

a. \(y = 2\cos \left( {x + \frac{\pi }{3}} \right) + 3\)

b.  \(y = \sqrt {1 - \sin \left( {{x^2}} \right)}  - 1\)

c.  \(y = 4\sin \sqrt x \)

Cho các hàm số f(x) = sinx, g(x) = cosx, h(x) = tanx và các khoảng

\(\begin{array}{l}
{J_1} = \left( {\pi ;\frac{{3\pi }}{2}} \right),{J_2} = \left( { - \frac{\pi }{4};\frac{\pi }{4}} \right),\\
{J_3} = \left( {\frac{{31\pi }}{4};\frac{{33\pi }}{4}} \right),{J_4} = \left( { - \frac{{452\pi }}{3};\frac{{601\pi }}{4}} \right)
\end{array}\)

Hỏi hàm số nào trong ba hàm số trên đồng biến trên khoảng J₁ ? Trên khoảng J₂ ? Trên khoảng J₃ ? Trên khoảng J₄ ? (Trả lời bằng cách lập bảng).

Trong các khẳng định sau, khẳng định nào đúng ? Khẳng định nào sai ? Giải thích vì sao ?

a. Trên mỗi khoảng mà hàm số y = sinx đồng biến thì hàm số y = cosx nghịch biến.

b. Trên mỗi khoảng mà hàm số y = sin²x đồng biến thì hàm số y = cos²x nghịch biến.

Cho hàm số y = f(x) = 2sin2x

a. Chứng minh rằng với số nguyên kk tùy ý, luôn có f(x+kπ) = f(x) với mọi x.

b. Lập bảng biến thiên của hàm số y = 2sin2x trên đoạn 

c. Vẽ đồ thị của hàm số y = 2sin2x

Xét tính chẵn – lẻ của mỗi hàm số sau:

a.  \(y = \cos \left( {x - \frac{\pi }{4}} \right)\)

b.  y = tan|x|

c.  y = tanx−sin2x

Cho các hàm số sau:

a. y = −sin²x

b.  y = 3tan²x+1

c. y = sinxcosx

d. \(y = \sin x.\cos x + \frac{{\sqrt 3 }}{2}\cos 2x\)

Chứng minh rằng mỗi hàm số y = f(x) đó đều có tính chất :

f(x+kπ) = f(x) với k ∈ Z, x thuộc tập xác định của hàm số f.

Cho hàm số y = f(x) = Asin(ωx+∝) (A, ωvà ∝ là những hằng số; A và ω khác 0). Chứng minh rằng với mỗi số nguyên k), ta có f(x+k.2πω) = f(x) với mọi x.

Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = \frac{x}{3}\) với đồ thị của hàm số y = sinx đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt {10} \).

Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:

a. y = −sinx

b.  y = |sinx|

c. y = sin|x|

a. Từ đồ thị của hàm số y = cosx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó:

y = cosx+2

\(y = \cos \left( {x - \frac{\pi }{4}} \right)\)

b. Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không ?

Xét hàm số  y = f(x) = \(\cos \frac{x}{2}\)

a. Chứng minh rằng với mỗi số nguyên k, f(x+k4π) = f(x) với mọi x.

b. Lập bảng biến thiên của hàm số y = \(\cos \frac{x}{2}\) trên đoạn [−2π;2π].

c. Vẽ đồ thị của các hàm số y = cosx và y = \(\cos \frac{x}{2}\) trong cùng một hệ trục tọa độ vuông góc Oxy.

d. Trong mặt phẳng tọa độ Oxy, xét phép biến hình F biến mỗi điểm (x;y) thành điểm (x′;y′) sao cho x′ = 2xvà y′ = y. Chứng minh rằng F biến đồ thị của hàm số y = cosx thành đồ thị của hàm số  y = \(\cos \frac{x}{2}\).

Giải các phương trình sau:

a) \(\sin 4x = \sin \frac{\pi }{5}\)

b) \(\sin \left( {\frac{{x + \pi }}{5}} \right) =  - \frac{1}{2}\)

c) \(\cos \frac{x}{2} = \cos \sqrt 2 \)

d) \(\cos \left( {x + \frac{\pi }{{18}}} \right) = \frac{2}{5}\)

a. Vẽ đồ thị của hàm số y = sinx rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng (−π;4π) là nghiệm của mỗi phương trình sau :

1.  \(\sin x =  - \frac{{\sqrt 3 }}{2}\)

2. sinx = 1

b. Cũng câu hỏi tương tự cho hàm số y = cosx đối với mỗi phương trình sau

1.  \(\cos x = \frac{1}{2}\)

2. cosx = −1.

Tìm nghiệm của các phương trình sau trong khoảng đã cho

a.  \(\sin 2x =  - \frac{1}{2}\) với 0 < x < π

b.  \(\cos \left( {x - 5} \right) = \frac{{\sqrt 3 }}{2}\) với −π < x < π

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40˚ bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số

\(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in Z,0 < t \le 365\).

a. Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm ?

b. Vào ngày nào trong năm thì thành phố A có ít giờ có ánh sáng mặt trời nhất ?

c. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất ?

Giải các phương trình sau:

a) \(\tan 3x = \tan \frac{{3\pi }}{5}\)

b) \(\tan \left( {x - {{15}^0}} \right) = 5\)

c) \(\tan \left( {2x - 1} \right) = \sqrt 3 \)

d) \(\cot 2x = \cot \left( { - \frac{1}{3}} \right)\)

e) \(\cot \left( {\frac{x}{4} + {{20}^0}} \right) =  - \sqrt 3 \)

f) \(\cot 3x = \tan \frac{{2\pi }}{5}\)

a. Vẽ đồ thị của hàm số y = tanx rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng (−π;π) là nghiệm của mỗi phương trình sau

1. tanx = −1

2. tanx = 0

b. Cũng câu hỏi tương tự cho hàm số y = cotx và cho mỗi phương trình sau

1.  \(\cot x = \frac{{\sqrt 3 }}{3}\)

2. cotx = 1

Tìm nghiệm của các phương trình sau trên khoảng đã cho

a. tan(2x−15⁰) = 1 với −180⁰ < x < 90⁰;

b. \(\cot 3x =  - \frac{1}{{\sqrt 3 }}\) với . 

Khi giải phương trình \(\tan x = \sqrt 3 \); bạn Phương nhận thấy \( - \sqrt 3  = \tan \left( { - \frac{\pi }{3}} \right)\) và viết \(\tan x =  - \sqrt 3  \Leftrightarrow \tan x = \tan \left( { - \frac{\pi }{3}} \right) \Leftrightarrow x =  - \frac{\pi }{3} + k\pi \).

Cũng phương trình đó, bạn Quyên lấy \( - \sqrt 3  = \tan \frac{{2\pi }}{3}\) nên giải như sau:

\(\begin{array}{l}
\tan x =  - \sqrt 3  \Leftrightarrow \tan x = \tan \frac{{2\pi }}{3}\\
 \Leftrightarrow x = \frac{{2\pi }}{3} + k\pi 
\end{array}\)

Theo em, ai giải đúng, ai giải sai ?

Tính các góc của tam giác ABC, biết \(AB = \sqrt 2 cm,AC = \sqrt 3 cm\) và đường cao AH = 1cm. (Gợi ý: Xét trường hợp B, C nằm khác phía đối với H và trường hợp B, C nằm cùng phía đối với H).

Tìm tập xác định của mỗi hàm số sau:

a) \(y = \frac{{1 - \cos x}}{{2\sin x + \sqrt 2 }}\)

b) \(y = \frac{{\sin \left( {x - 2} \right)}}{{\cos 2x - \cos x}}\)

c) \(y = \frac{{\tan x}}{{1 + \tan x}}\)

d) \(y = \frac{1}{{\sqrt 3 \cot 2x + 1}}\)

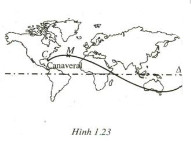
Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất

như hình 1.23: điểm M mô tả cho con tàu, đường thẳng Δ mô tả cho đường xích đạo.

Khoảng cách h (kilomet) từ M đến Δ được tính theo công thức h = |d|, trong đó:

\(d = 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right]\)

Với t (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, d > 0 nếu M ở phía trên Δ, d < 0 nếu M ở phía dưới Δ.

a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với t = 0). Hãy tính khoảng cách từ điểm C đến đường thẳng Δ, trong đó C là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.

b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = 2000.

c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = −1236.

(Tính chính xác các kết quả đến hàng phần nghìn).

Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (h.1.24). Khi guồng quay đều, khoảng cách h (mét) từ một chiếc gầu gắn tại điểm A của guồng đến mặt nước được tính theo công thức h = |y|, trong đó

\(y = 2 + 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right]\)

Với x là thời gian quay guồng (x ≥ 0), tính bằng phút ; ta quy ước rằng y > 0 khi gầu ở bên trên mặt nước và y < 0 khi gầu ở dưới nước (xem bài đọc thêm về dao động điều hòa trang 15). Hỏi :

a. Khi nào thì chiếc gầu ở vị trí thấp nhất ?

b. Khi nào thì chiếc gầu ở vị trí cao nhất ?

c. Chiếc gầu cách mặt nước 2m lần đầu tiên khi nào ?

Dùng công thức biến đổi tổng thành tích, giải các phương trình sau:

a) \(\cos 3x = \sin 2x\)

b) \(\sin \left( {x - {{120}^0}} \right) - \cos 2x = 0\)

Giải các phương trình sau:

a) \(2\cos x - \sqrt 3  = 0\)

b) \(\sqrt 3 \tan 3x - 3 = 0\)

c) \(\left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0\)

Giải các phương trình sau:

a) \(2{\cos ^2}x - 3\cos x + 1 = 0\)

b) \({\cos ^2}x + \sin x + 1 = 0\)

c) \(\sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0\)

Giải các phương trình sau trên khoảng đã cho rồi dùng bảng số hoặc máy tính bỏ túi để tính gần đúng nghiệm của chúng (tính chính xác đến hàng phần trăm):

a.  \(3\cos 2x + 10\sin x + 1 = 0\) trên \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)

b.  \(4\cos 2x + 3 = 0\) trên \(\left( {0;\frac{\pi }{2}} \right)\)

c.  \({\cot ^2}x - 3\cot x - 10 = 0\) trên (0;π)

d.  5−3tan3x = 0 trên \(\left( { - \frac{\pi }{6};\frac{\pi }{6}} \right)\)

Giải các phương trình sau:

a) \(3\cos x + 4\sin x =  - 5\)

b) \(2\sin 2x - 2\cos 2x = \sqrt 2 \)

c) \(5\sin 2x - 6{\cos ^2}x = 13\)

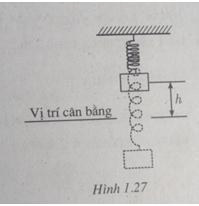
Một vật nặng treo bởi một chiếc lò xo chuyển động lên xuống qua vị trí cân bằng. Khoảng cách h từ vật đó đến vị trí cân bằng ở thời điểm t giây được tính theo công thức h = |d| trong đó d = 5sin6t–4cos6t với d được tính bằng xentimet, ta quy ước rằng d > 0 khi vật ở phía trên vị trí cân bằng, d < 0 khi vật ở phía dưới vị trí cân bằng. Hỏi:

a. Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng?

b. Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất?

(Tính chính xác đến \(\frac{1}{{100}}\) giây).

Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi biểu thức sau:

a. asinx+bcosx (a và b là hằng số, a²+b² ≠ 0) ;

b.  sin²x+sinxcosx+3cos²x;

c. Asin²x+Bsinxcosx+Ccos²x (A, B và C là hằng số).

Giải các phương trình sau:

a.  \(2{\sin ^2}x + 3\sqrt 3 \sin x\cos x - {\cos ^2}x = 4\)

b. \(3{\sin ^2}x + 4\sin 2x + \left( {8\sqrt 3  - 9} \right){\cos ^2}x = 0\)

c.  \({\sin ^2}x + \sin 2x - 2{\cos ^2}x = \frac{1}{2}\)

Sử dụng công thức biến đổi tổng thành tích hoặc tích thành tổng để giải các phương trình sau:

a) \(\cos x\cos 5x = \cos 2x\cos 4x\)

b) \(\cos 5x\sin 4x = \cos 3x\sin 2x\)

c) \(\sin 2x + \sin 4x = \sin 6x\)

d) \(\sin x + \sin 2x = \cos x + \cos 2x\)

Dùng công thức hạ bậc để giải các phương trình sau:

a) \({\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x\)

b) \({\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2\)

Giải các phương trình sau:

a. \(\tan \frac{x}{2} = \tan x\)

b.  \(\tan \left( {2x + {{10}^0}} \right) + \cot x = 0\)

c.  \(\left( {1 - \tan x} \right)\left( {1 + \sin 2x} \right) = 1 + \tan x\)

d.  tanx+tan2x = sin3xcosx

e.  tanx+cot2x = 2cot4x

Mùa xuân ở Hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động qua lại vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng (h. 1.32) được biểu diễn qua thời gian t (t ≥ 0 và được tính bằng giây) bởi hệ thức h = |d| với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp trái lại.

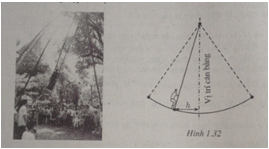
a. Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.

b. Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 mét (tính chính xác đến \(\frac{1}{{100}}\) giây).

Giải các phương trình sau:

a) \({\cos ^2}x - 3{\sin ^2}x = 0\)

b) \({\left( {\tan x + \cot x} \right)^2} - \left( {\tan x + \cot x} \right) = 2\)

c) \(\sin x + {\sin ^2}\frac{x}{2} = 0,5\)

Chứng minh rằng các phương trình sau đây vô nghiệm:

a. sinx–2cosx = 3

b. 5sin2x+sinx+cosx+6 = 0

Hướng dẫn b. Đặt sinx+cosx = t

Tìm các nghiệm của mỗi phương trình sau trong khoảng đã cho (khi cần tính gần đúng thì tính chính xác đến \(\frac{1}{{10}}\) giây)

a.  \(2{\sin ^2}x - 3\cos x = 2,{0^0} \le x \le {360^0}\)

b.  \(\tan x + 2\cot x = 3,\,\,{180^0} \le x \le {360^0}\)

Giải các phương trình sau:

a.  3sin²x−sin2x−cos²x = 0

b.  3sin²2x−sin2xcos2x−4cos²2x = 2

c.  \(2\sin 2x + \left( {3 + \sqrt 3 } \right)\sin x\cos x + \left( {\sqrt 3  - 1} \right)\cos 2x =  - 1\)

Giải các phương trình sau:

a) \(\sin x + \sin 2x + \sin 3x = \cos x + \cos 2x + \cos 3x\)

b) \(\sin x = \sqrt 2 \sin 5x - \cos x\)

c) \(\frac{1}{{\sin 2x}} + \frac{1}{{\cos 2x}} = \frac{2}{{\sin 4x}}\)

d) \(\sin x + \cos x = \frac{{\cos 2x}}{{1 - \sin 2x}}\)

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

a. Các hàm số y = sinx, y = cosx có cùng tập xác định.

b. Các hàm số y = tanx, y = cotx có cùng tập xác định.

c. Các hàm số y = sinx, y = tanx là những hàm số lẻ.

d. Các hàm số y = cosx, y = cotx là những hàm số chẵn.

e. Các hàm số y = sinx, y = cosx cùng nghịch biến trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)

f. Hàm số y = cosx nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)

g. Trên mỗi khoảng mà hàm số y = tanx đồng biến thì hàm số y = cotx nghịch biến.

Xét hàm số y = f(x) = sinπx.

a. Chứng minh rằng với mỗi số nguyên chẵn m ta có f(x+m) = f(x) với mọi x.

b. Lập bảng biến thiên của hàm số trên đoạn [−1;1].

c. Vẽ đồ thị của hàm số đó.

Đưa các biểu thức về dạng \(C\sin \left( {x + \alpha } \right)\):

a) \(\sin x + \tan \frac{\pi }{7}\cos x\)

b) \(\tan \frac{\pi }{7}\sin x + \cos x\)

Giải các phương trình sau:

a) \(\sin \left( {x - \frac{{2\pi }}{3}} \right) = \cos 2x\)

b) \(\tan \left( {2x + {{45}^0}} \right)\tan \left( {{{180}^0} - \frac{x}{2}} \right) = 1\)

c) \(\cos 2x - {\sin ^2}x = 0\)

d) \(5\tan x - 2\cot x = 3\)

Giải các phương trình sau:

a.  \(\sin 2x + {\sin ^2}x = \frac{1}{2}\)

b.  2sin2x+3sinxcosx+cos2x = 0

c.  \({\sin ^2}\frac{x}{2} + \sin x - 2{\cos ^2}\frac{x}{2} = \frac{1}{2}\)

a. Chứng minh rằng \(\sin \frac{\pi }{{12}} = \frac{{\sqrt 3  - 1}}{{2\sqrt 2 }}\)

b. Giải các phương trình \(2\sin x - 2\cos x = 1 - \sqrt 3 \) bằng cách biến đổi vế trái về dạng Csin(x+α)

c. Giải phương trình \(2\sin x - 2\cos x = 1 - \sqrt 3 \) bằng cách bình phương hai vế.

Giải phương trình:

\(\frac{{1 + \cos 2x}}{{\cos x}} = \frac{{\sin 2x}}{{1 - \cos 2x}}\)

Cho phương trình \(\frac{{{{\sin }^3}x + {{\cos }^3}x}}{{2\cos x - \sin x}} = \cos 2x\).

a. Chứng minh rằng \(x = \frac{\pi }{2} + k\pi \) nghiệm đúng phương trình.

b. Giải phương trình bằng cách đặt tanx = t (khi \(x \ne \frac{\pi }{2} + k\pi \))

Giá trị lớn nhất của các biểu thức \({\sin ^4}x + {\cos ^4}x\) là :

A. 0

B. 1

C. 2

D. \(\frac{1}{2}\)

Giá trị bé nhất của biểu thức \(\sin x + \sin \left( {x + \frac{{2\pi }}{3}} \right)\) là

A. -2

B. \(\frac{{\sqrt 3 }}{2}\)

C. -1

D. 0

Tập xác định của hàm số \(y = 2\sin 2x + 3\) là :

A. [0;1]

B. [2;3]

C. [−2;3]

D. [1;5]

Tập giá trị của hàm số \(y = 1--2|\sin 3x|\) là

A. [−1;1]

B. [0;1]

C. [−1;0]

D. [−1;3]

Giá trị lớn nhất của biểu thức \(y = {\cos ^2}x - \sin x\) là

A. 2

B. 0

C. \(\frac{5}{4}\)

D. 1

Trả lời

Tập giá trị của hàm số \(y = 4\cos 2x--3\sin 2x + 6\) là :

A. [3;10]

B. [6;10]

C. [−1;13]

D. [1;11]

Khi x thay đổi trong khoảng \(\left( {\frac{{5\pi }}{4};\frac{{7\pi }}{4}} \right)\) thì \(y = \sin x\) lấy mọi giá trị thuộc

A. \(\left[ {\frac{{\sqrt 2 }}{2};1} \right]\)

B. \(\left[ { - 1; - \frac{{\sqrt 2 }}{2}} \right]\)

C. \(\left[ { - \frac{{\sqrt 2 }}{2};0} \right]\)

D.  [−1;1]

Khi x thay đổi trong nửa khoảng \(\left( { - \frac{\pi }{3};\frac{\pi }{3}} \right]\) thì \(y = \cos x\) lấy mọi giá trị thuộc

A. \(\left[ {\frac{1}{2};1} \right]\)

B. \(\left( {\frac{1}{2};\frac{1}{2}} \right)\)

C. \(\left( { - \frac{1}{2};\frac{1}{2}} \right)\)

D. \([ - 1;\frac{1}{2}]\)

Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = 1\) thuộc đoạn \([\pi ;2\pi ]\) là

A. 1

B. 2

C. 3

D. 0

Số nghiệm của phương trình \(\sin \left( {2x + \frac{\pi }{4}} \right) =  - 1\) thuộc đoạn \([0;\pi ]\) là

A. 1

B. 2

C. 3

D. 0

Một nghiệm của phương trình 

\({\sin ^2}x + {\sin ^2}2x + {\sin ^2}3x = 2\) là

A.  \(\frac{\pi }{{12}}\)

B.  \(\frac{\pi }{3}\)

C.  \(\frac{\pi }{8}\)

D.  \(\frac{\pi }{6}\)

Số nghiệm của phương trình \(\cos \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = 0\) thuộc khoảng \((\pi ;8\pi )\) là

A. 1

B. 3

C. 2

D. 4

Số nghiệm của phương trình \(\frac{{\sin 3x}}{{\cos x + 1}} = 0\) thuộc đoạn \([2\pi ;4\pi ]\) là

A. 2

B. 4

C. 5

D. 6