Bài tập 22 trang 30 SGK Toán 11 NC

Bài tập 22 trang 30 SGK Toán 11 NC

Ta xét hai trường hợp:

• TH1: B và C nằm khác phía đối với H

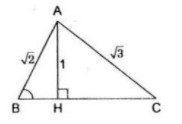
Trong tam giác vuông ABH ta có:

\(\sin B = \frac{{AH}}{{AB}} = \frac{1}{{\sqrt 2 }}\)      

Suy ra \(\widehat B = {45^0}\) (chú ý rằng góc B nhọn)

Trong tam giác ACH ta có:

\(\sin C = \frac{{AH}}{{AC}} = \frac{1}{{\sqrt 3 }}\), suy ra \(\widehat C \approx {35^0}15'52\)

Từ đó \(\widehat A = {180^0} - \left( {\widehat B + \widehat C} \right) \approx {99^0}44'8\)

• TH2: B và C nằm cùng phía đối với H

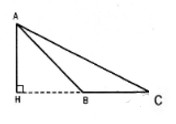
Tương tự như trên ta có:

\(\begin{array}{l}
\widehat {ABC} = {180^0} - \widehat {ABH} = {180^0} - {45^0} = {135^0}\\
\widehat C \approx {35^0}15'52
\end{array}\)

Từ đó \(\widehat A = {180^0} - \left( {\widehat B + \widehat C} \right) \approx {9^0}44'8\)

-- Mod Toán 11