Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Chương 1: Hàm Số Lượng Giác Và Phương Trình Lượng Giác
Bài tập 5 trang 17 SGK Đại số & Giải tích 11
Bài tập 5 trang 17 SGK Đại số & Giải tích 11
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 5 trang 17 SGK Đại số & Giải tích 11
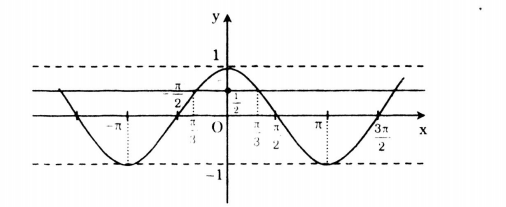
Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của x để cosx =  .
.
* Vẽ đồ thị hàm số y = cosx và đường thẳng \(y=\frac{1}{2}\) trên cùng một hệ trục toạ độ Oxy.
* Để \(cosx=\frac{1}{2}\) thì đường thẳng \(y=\frac{1}{2}\) cắt đồ thị y = cosx. Dựa vào đồ thị suy ra \(cosx=\frac{1}{2}\) khi \(x\in \left \{ ....;-\frac{7\pi }{3};-\frac{\pi }{3};\frac{\pi }{3};\frac{7\pi }{3};...\right \}\) hay \(x=\pm \frac{\pi }{3}+k2 \pi (k\in \mathbb{Z})\)
-- Mod Toán 11
Copyright © 2021 HOCTAP247