Bài tập 15 trang 28 SGK Toán 11 NC

Bài tập 15 trang 28 SGK Toán 11 NC

a)

\(1/\begin{array}{l}
\sin x =  - \frac{{\sqrt 3 }}{2} \Leftrightarrow {\rm{sinx}} = \sin \left( { - \frac{\pi }{3}} \right)\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - \frac{\pi }{3} + k2\pi }\\
{x = \frac{{4\pi }}{3} + k2\pi }
\end{array}} \right.
\end{array}\)

• Với \(x =  - \frac{\pi }{3} + k2\pi \) và x∈(−π;4π) ta có nghiệm:

\({x_1} =  - \frac{\pi }{3},{x_2} = \frac{{5\pi }}{3},{x_3} = \frac{{11\pi }}{3}\)

• Với \(x = \frac{{4\pi }}{3} + k2\pi \) và x∈(−π;4π) ta có nghiệm:

\({x_4} =  - \frac{{2\pi }}{3},{x_5} = \frac{{4\pi }}{3},{x_6} = \frac{{10\pi }}{3}\)

2/ \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \)

• Với \(x = \frac{\pi }{2} + k2\pi \) và x∈(−π;4π) ta có nghiệm :

\({x_1} = \frac{\pi }{2},{x_2} = \frac{{5\pi }}{2}\)

Xem hình vẽ

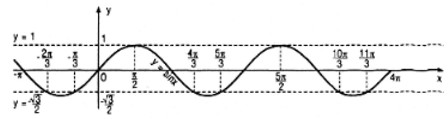
b) Tương tự câu a) ta có hình vẽ sau:

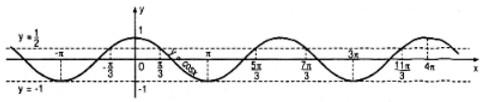
1. Nghiệm của phương trình \(\cos x = \frac{1}{2}\) thuộc khoảng (−π;4π) là:

\(\begin{array}{l}
{x_1} =  - \frac{\pi }{3},{x_2} = \frac{\pi }{3},{x_3} = \frac{{5\pi }}{3},\\
{x_4} = \frac{{7\pi }}{3},{x_5} = \frac{{11\pi }}{3}
\end{array}\)

2. Nghiệm của phương trình cosx = −1 thuộc khoảng (−π;4π) là :

\({x_1} =  - \pi ,{x_2} = \pi ,{x_3} = 3\pi \)

-- Mod Toán 11