Bài tập 10 trang 17 SGK Toán 11 NC

Bài tập 10 trang 17 SGK Toán 11 NC

Đường thẳng \(y = \frac{x}{3}\) đi qua các điểm E(−3;−1) và F(3;1)

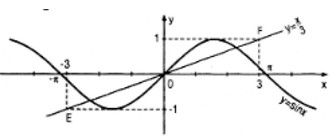
Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải {(x;y)|−1 ≤ y ≤ 1} (dải này chứa đồ thị của hàm số y = sinx). Vậy các giao điểm của đường thẳng \(y = \frac{x}{3}\) với đồ thị của hàm số y = sinx phải thuộc đoạn EF; mọi điểm của đoạn thẳng này cách O một khoảng dài hơn \(\sqrt {9 + 1}  = \sqrt {10} \) (và rõ ràng E, F không thuộc đồ thị của hàm số y = sinx). 

-- Mod Toán 11