Bài tập 12 trang 17 SGK Toán 11 NC

Bài tập 12 trang 17 SGK Toán 11 NC

a) Đồ thị của hàm số y = cosx+2 có được do tịnh tiến đồ thị của hàm số y = cosx lên trên một đoạn có độ dài bằng 2, tức là tịnh tiến theo vectơ \(2\overrightarrow j \,\) (\({\overrightarrow j  = \left( {0;1} \right)}\) là vecto đơn vị trên trục tung).

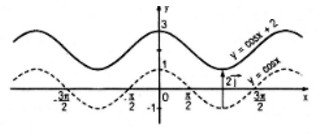
Đồ thị của hàm số \(y = \cos \left( {x - \frac{\pi }{4}} \right)\) có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài \(\frac{\pi }{4}\), tức là tịnh tiến theo vexto \({\frac{\pi }{4}}\) (\(\overrightarrow i  = \left( {1;0} \right)\) là vecto đơn vị trên trục hoành).

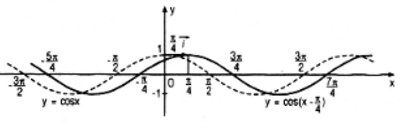
b) Các hàm số trên đều là hàm tuần hoàn vì:

Nếu f(x) = cosx+2 thì f(x+2π) = cos(x+2π)+2 = cosx+2 = f(x), ∀x ∈ R

Và nếu \(g\left( x \right) = \cos \left( {x - \frac{\pi }{4}} \right)\) thì:

\(\begin{array}{l}
g\left( {x + 2\pi } \right) = \cos \left( {x + 2\pi  - \frac{\pi }{4}} \right)\\
 = \cos \left( {x - \frac{\pi }{4}} \right) = g\left( x \right),\forall x \in R
\end{array}\)

-- Mod Toán 11