Bài tập 24 trang 32 SGK Toán 11 NC
Bài tập 24 trang 32 SGK Toán 11 NC
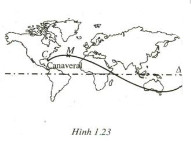
Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất
như hình 1.23: điểm M mô tả cho con tàu, đường thẳng Δ mô tả cho đường xích đạo.
Khoảng cách h (kilomet) từ M đến Δ được tính theo công thức h = |d|, trong đó:
\(d = 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right]\)
Với t (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, d > 0 nếu M ở phía trên Δ, d < 0 nếu M ở phía dưới Δ.
a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với t = 0). Hãy tính khoảng cách từ điểm C đến đường thẳng Δ, trong đó C là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.
b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = 2000.
c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có d = −1236.
(Tính chính xác các kết quả đến hàng phần nghìn).
a) Vì t = 0 nên \(d = 4000\cos \left( { - \frac{{10\pi }}{{45}}} \right) = 400\cos \frac{{2\pi }}{9}\). Do đó:
\(h = \left| d \right| \approx 3064,178\left( {km} \right)\)
b)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
d = 2000 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = 2000\\
\Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = \frac{1}{2}
\end{array}\\
{ \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) = \pm \frac{\pi }{3} + k2\pi }\\
{ \Leftrightarrow t = 10 \pm 15 + 90k}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 25 + 90k}\\
{t = - 5 + 90k}
\end{array}} \right.}
\end{array}\)
Chú ý rằng t > 0 ta thấy ngay giá trị nhỏ nhất của t là t = 25. Vậy d = 2000 (km) xảy ra lần đầu tiên sau khi phóng con tàu vào quỹ đạo được 25 phút.
c)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
d = - 1236 \Leftrightarrow 400\cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = - 1236\\
\Leftrightarrow \cos \left[ {\frac{\pi }{{45}}\left( {t - 10} \right)} \right] = - 0,309
\end{array}\\
{ \Leftrightarrow \frac{\pi }{{45}}\left( {t - 10} \right) = \pm \alpha + k2\pi \left( {k \in Z,cos\alpha = - 0,309} \right)}\\
{ \Leftrightarrow t = \pm \frac{{45}}{\pi }\alpha + 10 + 90k}
\end{array}\)
Sử dụng bảng số hoặc máy tính bỏ túi, ta có thể chọn \(\alpha \approx 1,885\). Khi đó ta có:
\(t \approx \pm 27,000 + 10 + 90k\), tức là \(t \approx - 17,000 + 90k\) hoặc \(t \approx 37,000 + 90k\)
Dễ thấy giá trị dương nhỏ nhất của tt là 37,000. Vậy d = −1236 (km) xảy ra lần đầu tiên là 37,000 phút sau khi con tàu được phóng vào quỹ đạo.
-- Mod Toán 11
Copyright © 2021 HOCTAP247
