Bài tập 71 trang 96 SGK Toán 9 Tập 2

Bài tập 71 trang 96 SGK Toán 9 Tập 2

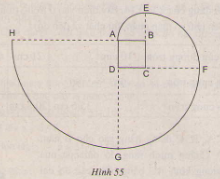
Với bài toán này, chúng ta sẽ vẽ lại hình và qua cách vẽ, ta tính được độ lớn của đường xoắn đề bài yêu cầu

Vẽ hình vuông ABCD có cạnh dài \(1cm\)

Vẽ  đường tròn tâm B, bán kính \(\small 1 cm\), ta có cung \(\widehat{AE}\)

Vẽ  đường tròn tâm C, bán kính \(\small 2 cm\), ta có cung  \(\widehat{EF}\)

Vẽ  đường tròn tâm D, bán kính \(\small 3 cm\), ta có cung \(\widehat{FG}\)

Vẽ  đường tròn tâm A, bán kính \(\small 4 cm\), ta có cung \(\widehat{GH}\)

Độ dài đường xoắn:

\(\l _{\widehat{AE}}=\frac{1}{4}2 \pi.1(cm)\)

\(\l _{\widehat{EF}}=\frac{1}{4}2 \pi.2(cm)\)

\(\l _{\widehat{FG}}=\frac{1}{4}2 \pi.3(cm)\)

\(\l _{\widehat{GH}}=\frac{1}{4}2 \pi.4(cm)\)

Vậy độ dài đường xoắn đề yêu cầu là:

= \(l_{ABCDEFGH}=\l _{\widehat{AE}}+\l _{\widehat{EF}}+\l _{\widehat{EG}}+\l _{\widehat{GH}}= \frac{1}{4}. 2\pi (1+2+3+4) = 5\pi(cm)\)

-- Mod Toán 9