Bài tập 83 trang 99 SGK Toán 9 Tập 2
Bài tập 83 trang 99 SGK Toán 9 Tập 2
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = 2cm. Nêu cách vẽ.
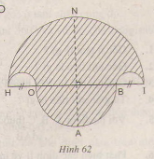
b) Tính diện tích hình HOABINH (miền gạch sọc)
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó.
Với bài 83, chúng ta sẽ tìm hiểu xem cách vẽ hình đã cho như thế nào và tính toán các giá trị đại số bằng công thức đã học.
Câu a:
.png)
Vẽ nửa đường tròn đường kính \(\small HI = 10 cm\)
Trên đường kính HI lấy điểm O và điểm B sao cho \(\small HO = BI = 2cm\)
Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn đường kính HI.
A là điểm chính giữa cung OB, N là điểm chính giữa cung HI
Chúng ta có hình vẽ như đề bài
Câu b:
Diện tích hình HOABINH là:
\(\small S=\frac{1}{2}\pi. 5^2-2.\frac{1}{2}.1^2.\pi+\frac{1}{2}\pi. 3^2=16\pi(cm^2)\)
Câu c:
Ta có độ dài NA là:
\(\small NA=\frac{HI}{2}+\frac{OB}{2}=8(cm)\)
Diện tích hình tròn đường kính NA là:
\(\small S=\left (\frac{8}{2} \right )^2.\pi=16\pi(cm^2)\)
Bài toán được giải quyết!
-- Mod Toán 9
Copyright © 2021 HOCTAP247
