Bài tập 85 trang 100 SGK Toán 9 Tập 2

Bài tập 85 trang 100 SGK Toán 9 Tập 2

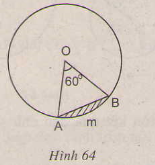
Với bài 85 này, chúng ta sẽ được biết thêm khái niệm về hình viên phân, rất dễ dàng thấy rằng diện tích ấy bằng diện tích quạt trừ diện tích tam giác OAB.

Gọi H là chân đường vuông góc từ O đến AB.

Vậy H là trung điểm AB

OAB là tam giác đều có cạnh bằng \(\small R = 5,1cm\)

\(\small \Rightarrow AH=\frac{5,1}{2}=2,55(cm)\)

\(\small \Rightarrow OH=\sqrt{OA^2-AH^2}=2,55\sqrt{3}(cm)\)

Vậy diện tích của tam giác AOB đều là:

\(\small S_{AOB}=\frac{1}{2}OH.AB=2,55.5,1\sqrt{3}.\frac{1}{2}=\approx 11,26(cm^2)\)

Diện tích quạt tròn AOB là:

\(\small S_q=\frac{\pi 5,1^2}{6}\approx 13,62(cm^2)\)

Diện tích viên phân cần tính là:

\(\small S=S_q-S_{ABC}\approx2,35(cm^2)\)

-- Mod Toán 9