Bài tập 3 trang 118 SGK Hình học 10 NC

Bài tập 3 trang 118 SGK Hình học 10 NC

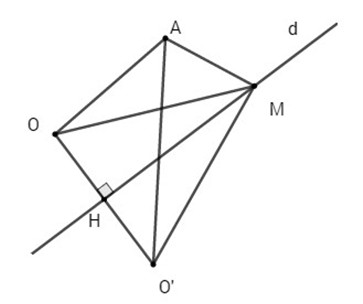
a) Điểm M và O nằm cùng phía đối với d khi và chỉ khi

(x−y+2).(0−0+2) > 0 ⇔ x−y+2 > 0

Ta có : x_A−y_A+2 = 2−0+2 = 4 > 0, do đó A nằm trong nửa mặt phẳng có bờ là d và chứa O.

b) Gọi d’ là đường thẳng qua O và vuông góc với d thì phương trình tổng quát của d’ là  d′: x+y = 0. Gọi H là hình chiếu của O lên d thì tọa độ H là nghiệm của hệ:

\(\left\{ \begin{array}{l}
x - y =  - 2\\
x + y = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  - 1\\
y = 1
\end{array} \right.\)

Vậy H(−1;1)

Gọi O’ là điểm đối xứng của O qua d thì H là trung điểm của OO’ do đó

\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{{x_H} = \frac{{{x_O} + {x_{O'}}}}{2}}\\
{{y_H} = \frac{{{y_O} + {y_{O'}}}}{2}}
\end{array}} \right.\\
 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_{O'}} = 2{x_H} - {x_O} =  - 2}\\
{{y_{O'}} = 2{y_H} - {x_O} = 2}
\end{array}} \right.
\end{array}\)

Vậy O′(−2;2)

c) OA không đổi nên chu vi tam giác AMO nhỏ nhất  khi tổng MO+MA nhỏ nhất.

Ta có: MO = MO′ ⇒ MO+MA = MO′+MA ≥ AO′

⇒ MO+MA nhỏ nhất khi A, M, O’ thẳng hàng, khi đó M là giao điểm của d với đường thẳng O’A.

Phương trình O’A:

\(\begin{array}{l}
\frac{{x - {x_A}}}{{{x_{O'}} - {x_A}}} = \frac{{y - {y_A}}}{{{y_{O'}} - {y_A}}}\\
 \Leftrightarrow \frac{{x - 2}}{{ - 2 - 2}} = \frac{{y - 0}}{{2 - 0}}\\
 \Leftrightarrow x + 2y - 2 = 0
\end{array}\)

Tọa độ M là nghiệm của hệ: 

\(\left\{ \begin{array}{l}
x - y =  - 2\\
x + 2y = 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x =  - \frac{2}{3}\\
y = \frac{4}{3}
\end{array} \right.\)

Vậy \(M\left( { - \frac{2}{3};\frac{4}{3}} \right)\)

-- Mod Toán 10