Bài tập 13 trang 120 SGK Hình học 10 NC
Bài tập 13 trang 120 SGK Hình học 10 NC
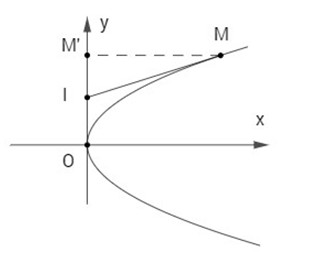
Cho parabol (P): y2 = 2px. Với mỗi điểm M trên (P) (M khác O), gọi M’ là hình chiếu của M trên Oy và I là trung điểm của đoạn OM’. Chứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất.
Giả sử M(xo;yo) ∈ (P) ta có y2o = 2pxo (xo ≠ 0) . M’ là hình chiếu của M trên Oy nên M′(0;yo), khi đó:
\(I\left( {0;\frac{{{y_0}}}{2}} \right) \Rightarrow \overrightarrow {IM} = \left( {{x_0};\frac{{{y_0}}}{2}} \right)\)
là vectơ chỉ phương của đường thẳng IM.
Phương trình tham số của IM là:
\(\left\{ \begin{array}{l}
x = {x_0}t\\
y = \frac{{{y_0}}}{2} + \frac{{{y_0}}}{2}t
\end{array} \right.\)
Thay x, y trong phương trình tham số của IM vào phương trình của (P) ta được:
\(\frac{{y_0^2}}{4}\left( {1 + {t^2}} \right) = 2p{x_0}t\)
mà 2pxo = y2o nên y2o(1+t2) = 4y2ot ⇔ (1+t2) = 4t ( do yo ≠ 0)
⇔ (t−1)2 = 0 ⇔ t = 1
Vậy IM cắt (P) tại điểm duy nhất M(xo;yo).
-- Mod Toán 10
Copyright © 2021 HOCTAP247