Bài tập 9 trang 119 SGK Hình học 10 NC

Bài tập 9 trang 119 SGK Hình học 10 NC

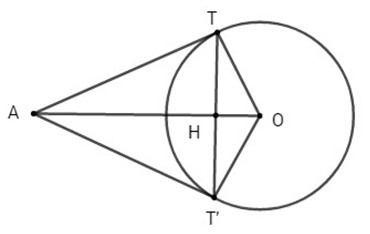
Đường tròn (C) có tâm O(0;0), bán kính R = 2.

a) Đường thẳng Δ qua A có dạng: 

a(x+2)+b(y−3) = 0 ⇔ ax+by+2a−3b = 0

Δ là tiếp tuyến của (C) \( \Leftrightarrow d\left( {O;\Delta } \right) = R\)

\(\begin{array}{l}
 \Leftrightarrow \frac{{\left| {2a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\\
 \Leftrightarrow {\left( {2a - 3b} \right)^2} = 4\left( {{a^2} + {b^2}} \right)\\
 \Leftrightarrow 5{b^2} - 12ab = 0\\
 \Leftrightarrow b\left( {5b - 12a} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
b = 0\\
12a = 5b
\end{array} \right.
\end{array}\)

Với b = 0, chọn a = 1 ta có tiếp tuyến Δ₁: x+2 = 0

Với 12a = 5b, chọn a = 5, b = 12 ta có tiếp tuyến Δ₂: 5x+12y−26 = 0

b) Gọi T, T’ là tiếp điểm của Δ₁, Δ₂ với (C) . Ta có:

\(AT = AT' = \sqrt {A{O^2} - {R^2}}  = \sqrt {13 - 4}  = 3\)

Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có:

\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{1}{{T{H^2}}} = \frac{1}{{A{T^2}}} + \frac{1}{{T{O^2}}}\\
 = \frac{1}{9} + \frac{1}{4} = \frac{{13}}{{36}}
\end{array}\\
\begin{array}{l}
 \Rightarrow TH = \frac{6}{{\sqrt {13} }}\\
 \Rightarrow TT' = 2TH = \frac{{12}}{{\sqrt {13} }}
\end{array}
\end{array}\)

-- Mod Toán 10