Bài tập 10 trang 119 SGK Hình học 10 NC
Bài tập 10 trang 119 SGK Hình học 10 NC
Cho \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) và hypebol \(\left( H \right):\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1\).
a) Tìm tọa độ các tiêu điểm của (E) và (H).
b) Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.
c) Tìm tọa độ các giao điểm của (E) và (H).
a) Với \(\left( E \right):\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) ta có:
\(a = \sqrt 5 ,b = 2 \Rightarrow c = \sqrt {{a^2} - {b^2}} = 1\)
Tọa độ các tiêu điểm của (E) là F1(−1;0), F2(1;0)
Với \(\left( H \right):\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1\), ta có:
\(a = \sqrt 5 ,b = 2 \Rightarrow c = \sqrt {{a^2} + {b^2}} = 3\)
Tọa độ các tiêu điểm của (H) là F1(−3;0), F2(3;0)
b) Vẽ (E) và (H).
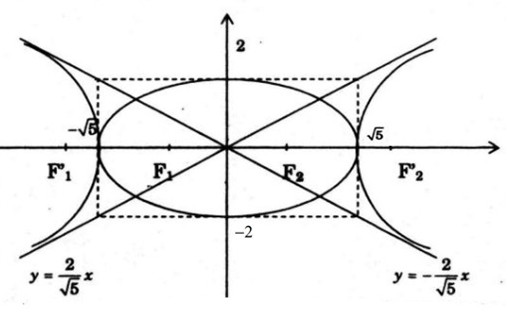
Câu c:
Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1}\\
{\frac{{{x^2}}}{5} - \frac{{{y^2}}}{4} = 1}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x^2} = 5}\\
{{y^2} = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \pm \sqrt 5 }\\
{y = 0}
\end{array}} \right.
\end{array}\)
Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 ;0} \right)\) và \(\left( {-\sqrt 5 ;0} \right)\).
-- Mod Toán 10
Copyright © 2021 HOCTAP247
