Chương 3: Phương Trình, Hệ Phương Trình.

Cho hai phương trình \(3x = 2\) và \(2x = 3.\)

Cộng các vế tương ứng của hai phương trình đã cho. Hỏi

a) Phương trình nhận được có tương đương với một trong hai phương trình đã cho hay không?

b) Phương trình đó có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không ?

Cho hai phương trình \(4x = 5\) và \(3x = 4\) .

Nhân các vế tương ứng của hai phương trình đã cho. Hỏi

a) Phương trình nhận được có tương đương với một trong hai phương trình đã cho hay không?

b) Phương trình đó có phải là phương trình hệ quả của một trong hai phương trình đã cho hay không?

Giải các phương trình 

a) \(\sqrt{3-x}+x =\)  \(\sqrt{3-x} + 1\);

b)  \(x +\sqrt{x-2}=\) \(\sqrt{2-x}+2\) ;

c) \(\frac{x^{2}}{\sqrt{x-1}}=\frac{9}{\sqrt{x-1}}\);

d)    \(x^2 -\sqrt{1-x}=\sqrt{x-2}+3\).

Giải các phương trình 

a)   \(x + 1 +\frac{2}{x +3}=\)  \(\frac{x +5}{x +3}\);

b)  \(2x +\frac{3}{x -1}=\) \(\frac{3x}{x -1}\);

c) \(\frac{x^{2}-4x-2}{\sqrt{x-2}}=\sqrt{x-2}\)

d) \(\frac{2x^{2}-x-3}{\sqrt{2x-3}}=\sqrt{2x-3}\).

Giải các phương trình

a) \(\frac{x^{2}+3x+2}{2x +3}=\) \(\frac{2x -5}{4}\);

b) \(\frac{2x +3}{x - 3}-\frac{4}{x+3}=\frac{24}{x^{2}-9} + 2\) ;

c) \(\sqrt{3x - 5}= 3\) ;

d) \(\sqrt{2x + 5}= 2\) .

Giải và biện luận các phương trình sau theo tham số m

a) \(m(x - 2) = 3x + 1\);

b) \(m^2x + 6 = 4x + 3m\);

c) \((2m + 1)x - 2m = 3x - 2\).

Có hai rổ quýt chứa số quýt bằng nhau. Nếu lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ hai bằng  của bình phương số quả còn lại ở rổ thứ nhất. Hỏi số quả quýt ở mỗi rổ lúc ban đầu là bao nhiêu ?

Giải các phương trình

a) \(2x^4 -7x^2 + 5 = 0\);

b) \(3x^4 + 2x^2 - 1 = 0\).

Giải các phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ ba)

a) \(2x^2 - 5x + 4 = 0\);

b) \(-3x^2 + 4x + 2 = 0\);

c) \(3x^2 + 7x + 4 = 0\);

d) \(9x^2 - 6x - 4 = 0\). 

Giải các phương trình.

a) \(|3x - 2| = 2x + 3\);

b) \(|2x -1| = |-5x - 2|\);

c) \(\frac{x-1}{2x -3}=\frac{-3x+1}{|x+1|};\)

d) \(|2x + 5| = x^2 +5x +1.\)

Giải các phương trình 

a) \(\sqrt{5x +6} = x - 6;\)

b)   \(\sqrt{3 -x}=\sqrt{x +2}+1;\) 

c) \(\sqrt{2x^{2} +5}= x + 2.\) 

d) \(\sqrt{4x^{2} +2x + 10} = 3x + 1.\)

Cho phương trình \(3x^2 - 2(m + 1)x + 3m - 5 = 0.\)

Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.

Cho hệ phương trình \(\left\{\begin{matrix} 7x - 5 y = 9 & \\ 14x - 10y = 10& \end{matrix}\right.\). Tại sao không cần giải ta cũng kết luận được hệ phương trình này vô nghiệm ?

Giải các hệ phương trình

a) \(\left\{\begin{matrix} 2x - 3y = 1 & \\ x + 2y = 3;& \end{matrix}\right.\)

b) \(\left\{\begin{matrix} 3x + 4y = 5 & \\ 4x - 2y = 2;& \end{matrix}\right.\)

c) \(\left\{ \begin{array}{l}\frac{2}{3}x + \frac{1}{2}y = \frac{2}{3}\\\frac{1}{3}x - \frac{3}{4}y = \frac{1}{2}\end{array} \right.\)

d) \(\left\{ \begin{array}{l}0,3x - 0,2y = 0,5\\0,5x + 0,4y = 1,2.\end{array} \right.\) 

Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền là 17 800 đồng. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18 000 đồng. Hỏi giá tiền mỗi quả quýt và mỗi quả cam là bao nhiêu?

Trong một xí nghiệp may có hai dây chuyền may áo sơ mi. Ngày thứ nhất cả hai dây chuyền may được 930 áo. Ngày thứ hai do dây chuyền thứ nhất tăng năng suất 18%, dây chuyền thứ hai tăng năng suất 15% nên cả hai dây chuyền may được 1083 áo. Hỏi trong ngày thứ nhất mỗi dây chuyền may được bao nhiêu áo sơ mi?

Giải các hệ phương trình

a) \(\left\{\begin{matrix} x + 3y + 2z =8 & \\ 2x + 2y + z =6& \\ 3x +y+z=6;& \end{matrix}\right.\)

b) \(\left\{\begin{matrix} x - 3y + 2z =-7 & \\ -2x + 4y + 3z =8& \\ 3x +y-z=5.& \end{matrix}\right.\)

Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu là 5 349 000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5 600 000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5 259 000 đồng. Hỏi giá bán mỗi áo, mỗi quần và mỗi váy là bao nhiêu?

Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai)

a) \(\left\{\begin{matrix} 3x - 5y = 6 & \\ 4x + 7y =-8;& \end{matrix}\right.\)

b) \(\left\{\begin{matrix} -2x +3y = 5 & \\ 5x +2y = 4.& \end{matrix}\right.\)

c) \(\left\{\begin{matrix} 2x - 3y +4z=-5 & \\ -4x +5y-z=6& \\ 3x+4y-3z=7; & \end{matrix}\right.\)

d) \(\left\{\begin{matrix} -x+2y-3z=2 & \\ 2x +y+2z=-3& \\ -2x-3y+z=5. & \end{matrix}\right.\)

Khi nào hai phương trình được gọi là tương đương? Cho ví dụ.

Thế nào là phương trình hệ quả? Cho ví dụ.

Giải các phương trình

a) \(\sqrt {x - 5}  + x = \sqrt {x - 5}  + 6\)            b) \(\sqrt {1 - x}  + x = \sqrt {x - 1}  + 2\)

c) \(\frac{{{x^2}}}{{\sqrt {x - 2} }} = \frac{8}{{\sqrt {x - 2} }}\)            d) \(3 + \sqrt {2 - x}  = 4{x^2} - x + \sqrt {x - 3} \)

Giải các phương trình
a) \(\frac{{3x + 4}}{{x - 2}} - \frac{1}{{x + 2}} = \frac{4}{{{x^2} - 4}} + 3\) 
b) \(\frac{{3{x^2} - 2x + 3}}{{2x - 1}} = \frac{{3x - 5}}{2}\) 
c) \(\sqrt {{x^2} - 4}  = x - 1\)

Giải các hệ phương trình:

a) \(\left\{ \begin{array}{l} - 2x + 5y = 9\\4x + 2y = 11\end{array} \right.\)

b) \(\left\{ \begin{array}{l}3x + 4y = 12\\5x - 2y = 7\end{array} \right.\)

c) \(\left\{ \begin{array}{l}2x - 3y = 5\\3x + 2y = 8\end{array} \right.\)

d) \(\left\{ \begin{array}{l}5x + 3y = 15\\4x - 5y = 6\end{array} \right.\)

Hai công nhân được giao việc sơn một bức tường. Sau khi người thứ nhất làm được 7 giờ và người thứ hai làm được 4 giờ thì họ sơn được \(\frac{5}{9}\) bức tường. Sau đó họ cùng làm việc với nhau trong 4 giờ thì chỉ còn lại \(\frac{1}{{18}}\) bức tường chưa sơn. Hỏi nếu mỗi người làm riêng thì sau bao nhiêu giờ mỗi người mới sơn xong bức tường?

Giải các hệ phương trình

a) \(\left\{ \begin{array}{l}2x - 3y + z =  - 7\\ - 4x + 5y + 3z = 6\\x + 2y - 2z = 5\end{array} \right.\)

b) \(\left\{ \begin{array}{l}x + 4y - 2z = 1\\ - 2x + 3y + z =  - 6\\3x + 8y - z = 12\end{array} \right.\)

Ba phân số đều có tử số là 1 và tổng của ba phân số đó bằng 1. Hiệu của phân số thứ nhất và phân số thứ hai bằng phân số thứ ba, còn tổng của phân số thứ nhất và phân số thứ hai bằng 5 lần phân số thứ ba. Tìm các phân số đó.

Một phân xưởng được giao sản xuất 360 sản phẩm trong một số ngày nhất định. Vì phân xưởng tăng năng suất, mỗi ngày làm thêm được 9 sản phẩm so với định mức, nên trước khi hết hạn một ngày thì phân xưởng đã làm vượt số sản phẩm được giao là 5%. Hỏi nếu vẫn tiếp tục làm việc với năng suất đó thì khi hết hạn phân xưởng đó làm được tất cả bao nhiêu sản phẩm.

Giải các phương trình sau bằng máy tính bỏ túi

a) \(5{x^2} - 3x - 7 = 0\)             b) \(3{x^2} + 4x + 1 = 0\)

c) \(0,2{x^2} + 1,2x - 1 = 0\)      d) \(\sqrt 2 {x^2} + 5x + \sqrt 8  = 0\)

Giải các phương trình:

a) \(|4x - 9|\,\, = \,\,3 - 2x\)                          b) \(|2x + 1|\,\, = \,\,|3x + 5|\)

Tìm hai cạnh của một mảnh vườn hình chữ nhật trong hai trường hợp.

a) Chu vi là 94,4m và diện tích là \(494,55{m^2}\)

b) Hiệu của hai cạnh là 12,1m và diện tích là 1089 \({m^2}\)

Hai người quét sân. Cả hai người cùng quét sân hết 1 giờ 20 phút, trong khi nếu chỉ quét một mình thì người thứ nhất quét hết nhiều hơn 2 giờ so với người thứ hai. Hỏi mỗi người quét sân một mình thì hết mấy giờ?

Tìm điều kiện xác định của mỗi phương trình sau rồi suy ra tập nghiệm của nó.

a) \(\sqrt x  = \sqrt { - x} \)

b) \(3x - \sqrt {x - 2}  = \sqrt {2 - x}  + 6\)

c) \(\frac{{\sqrt {3 - x} }}{{x - 3}} = x + \sqrt {x - 3} \)

d) \(x + \sqrt {x - 1}  = \sqrt { - x} \)

Giải các phương trình sau:

a) \(x + \sqrt {x - 1}  = 2 + \sqrt {x - 1} \)

b) \(x + \sqrt {x - 1}  = 0,5 + \sqrt {x - 1} \)

c) \(\frac{x}{{2\sqrt {x - 5} }} = \frac{3}{{\sqrt {x - 5} }}\)

d) \(\frac{x}{{2\sqrt {x - 5} }} = \frac{2}{{\sqrt {x - 5} }}\)

Giải các phương trình sau:

a) \(x + \frac{1}{{x - 1}} = \frac{{2x - 1}}{{x - 1}}\)

b) \(x + \frac{1}{{x - 2}} = \frac{{2x - 3}}{{x - 2}}\)

c) \(\left( {{x^2} - 3x + 2} \right)\sqrt {x - 3}  = 0\)

d) \(\left( {{x^2} - x - 2} \right)\sqrt {x + 1}  = 0\)

Giải các phương trình sau bằng cách bình phương hai vế của phương trình.

a) \(\sqrt {x - 3}  = \sqrt {9 - 2x} \)

b) \(\sqrt {x - 1}  = x - 3\)

c) \(2\left| {x - 1} \right| = x + 2\)

d) \(\left| {x - 2} \right| = 2x - 1\)

Xem các bài giải sau đây và cho biết mỗi bài giải đó đúng hay sai? Vì sao?

a) \(\frac{{\left( {x - 2} \right)\left( {x - 1} \right)}}{{\sqrt x  - 1}} = 0\)

\(\begin{array}{l}
 \Leftrightarrow \frac{{x - 2}}{{\sqrt x  - 1}}\left( {x - 1} \right) = 0\\
 \Leftrightarrow \left[ \begin{array}{l}
\frac{{x - 2}}{{\sqrt x  - 1}} = 0\\
x - 1 = 0
\end{array} \right.
\end{array}\)

Ta có \(\frac{{x - 2}}{{\sqrt x  - 1}} = 0 \Leftrightarrow x = 2\)

\(x - 1 = 0 \Leftrightarrow x = 1\)

Vậy tập nghiệm của phương trình đã cho là S = {1, 2}

b) \(\sqrt {{x^2} - 2}  = 1 - x \)

\(\Leftrightarrow {x^2} - 2 = {\left( {1 - x} \right)^2}\)

\(\begin{array}{l}
 \Leftrightarrow {x^2} - 2 = 1 - 2x + {x^2}\\
 \Leftrightarrow 2x = 3 \Leftrightarrow x = \frac{3}{2}
\end{array}\)

Vậy phương trình có nghiệm \(x = \frac{3}{2}\)

Giải và biện luận các phương trình

a) \((m^2+2)x-2m=x-3\)

b) \(m(x-m)=x+m-2\)

c) \(m(x-m+3)=m(x-2)+6\)

d) \(m^2(x-1)+m=x(3m-2)\)

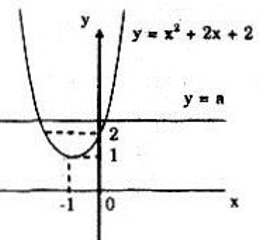
Dựa vào hình bên, tìm các giá trị của a để phương trình: \(3x+2=−x^2+x+a\) có nghiệm dương.

Khi đó, hãy tìm nghiệm dương của phương trình.

Giải và biện luận các phương trình

a) \((m-1)x^2+3x-1=0\)

b) \(x^2-4x+m-3=0\)

a) Giả sử phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1 và x2.

Chứng minh rằng:  ax2 + bx + c = a(x – x1)(x – x2)

b) Áp dụng: Phân tích các đa thức sau thành nhân tử

\(f(x)=-2x^2-7x+4\);

\(g\left( x \right) = \left( {\sqrt 2  + 1} \right){x^2} - 2\left( {\sqrt 2  + 1} \right)x + 2\)

Không giải phương trình x² - 2x - 15 = 0, hãy tính:

a) Tổng các bình phương hai nghiệm của nó.

b) Tổng các lập phương hai nghiệm của nó.

c) Tổng các lũy thừa bậc bốn hai nghiệm của nó.

Hướng dẫn: 

\(x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2\)

Trong các khẳng định sau đây có duy nhất khẳng định đúng. Hãy chọn khẳng định đó. Phương trình: \(\left( {\sqrt 3  - 1} \right){x^4} + {x^2} + 2\left( {1 - \sqrt 3 } \right) = 0\).

(A) Vô nghiệm;

(B) Có hai nghiệm \(x =  \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 }  - 1} \right)} \);

(C) Có bốn nghiệm \(x =  \pm \frac{1}{2}\sqrt {\left( {1 + \sqrt 3 } \right)\left( {\sqrt {33 - 16\sqrt 3 }  - 1} \right)} \) và \(x =  \pm \sqrt 3 \)

(D) Có hai nghiệm \(x =  \pm \sqrt 3 \)

Giải và biện luận các phương trình sau (m là tham số):

a) 2(m + 1)x - m(x - 1) = 2m + 3;

b) m²(x - 1) + 3mx = (m² + 3)x - 1;

c) 3(m + 1)x + 4 = 2x + 5(m + 1);

d) m²x + 6 = 4x + 3m.

a) Tìm các giá trị của p để phương trình sau vô nghiệm:

(p + 1)x – (x + 2) = 0

b) Tìm p để phương trình: p²x - p = 4x – 2 có vô số nghiệm

Tìm nghiệm gần đúng của phương trình sau chính xác đến hàng phần trăm.

a) \(x^2-5,6x+6,41=0\);

b) \(\sqrt 2 {x^2} + 4\sqrt 3 x - 2\sqrt 2  = 0\)

Tìm độ dài các cạnh của một tam giác vuông, biết rằng cạnh dài nhất hơn cạnh dài thứ hai là 2m, cạnh dài thứ hai hơn cạnh ngắn nhất là 23m.

Giải và biện luận các phương trình sau (m và k là tham số),

a) (m - 1)x² + 7x - 12 = 0;

b) mx² - 2(m + 3)x + m + 1 = 0;

c) [(k + 1)x - 1](x - 1) = 0;

d) (mx - 2)(2mx - x + 1) = 0.

Biện luận số giao điểm của hai parabol y = - x² - 2x + 3 và y = x² - m theo tham số m.

Tìm các giá trị của m để phương trình x² - 4x + m - 1 = 0 có hai nghiệm x₁ và x₂ thỏa mãn hệ thức x₁³ + x₂³ = 40.

Giải phương trình x² + (4m + 1)x + 2(m - 4) = 0, biết rằng nó có hai nghiệm và hiệu giữa nghiệm lớn và nghiệm nhỏ bằng 17.

Không giải phương trình, hãy xét xem mỗi phương trình trùng phương sau có bao nhiêu nghiệm

a) x⁴ + 8x² + 12 = 0;

b) -1,5x⁴ - 2,6x² + 1 = 0;

c) \(\left( {1 - \sqrt 2 } \right){x^4} + 2{x^2} + 1 - \sqrt 2  = 0\)

d) \( - {x^4} + \left( {\sqrt 3  - \sqrt 2 } \right){x^2} = 0\)

Cho phương trình: kx² - 2(k + 1)x + k + 1 = 0.

a) Tìm k để phương trình trên có ít nhất một nghiệm dương.

b) Tìm các giá trị của k để phương trình trên có một nghiệm lớn hơn 1 và một nghiệm nhỏ hơn 1.

(Hướng dẫn: Đặt x = y + 1).

Giải các phương trình

a) \(\frac{{2\left( {{x^2} - 1} \right)}}{{2x + 1}} = 2 - \frac{{x + 2}}{{2x + 1}}\)

b) \(\frac{{2x - 5}}{{x - 1}} = \frac{{5x - 3}}{{3x + 5}}\)

Giải phương trình sau \(\frac{{m - 3}}{{x - 4}} = {m^2} - m - 6\) trong mỗi trường hợp sau:

a) m = 3

b) m ≠ 3

Giải và biện luận các phương trình (a và m là những tham số)

a) \(\left| {2ax + 3} \right| = 5\)

b) \(\frac{{2mx - {m^2} + m - 2}}{{{x^2} - 1}} = 1\)

Giải và biện luận các phương trình (m, a và k là tham số)
a) \(\left| {mx - x + 1} \right| = \left| {x + 2} \right|\)

b) \(\frac{a}{{x + 2}} + \frac{1}{{x - 2a}} = 1\)

c) \(\frac{{mx - m - 3}}{{x + 1}} = 1\)

d) \(\frac{{3x + k}}{{x - 3}} = \frac{{x - k}}{{x + 3}}\)

Giải và biện luận phương trình sau (m và a là những tham số)

a) \(\left( {2x + m - 4} \right)\left( {2mx - x + m} \right) = 0\)

b) \(\left| {mx + 2x - 1} \right| = \left| x \right|\)

c) \(\left( {mx + 1} \right)\sqrt {x - 1}  = 0\)

d) \(\frac{{2a - 1}}{{x - 2}} = a - 2\)

e) \(\frac{{\left( {m + 1} \right)x + m - 2}}{{x + 3}} = m\)

f) \(\left| {\frac{{ax + 1}}{{x - 1}}} \right| = a\)

Bằng cách đặt ẩn phụ, giải các phương trình sau:

a) \(4{x^2} - 12x - 5\sqrt {4{x^2} - 12x + 11}  + 15 = 0\)

b) \({x^2} + 4x - 3\left| {x + 2} \right| + 4 = 0\)

c) \(4{x^2} + \frac{1}{{{x^2}}} + \left| {2x - \frac{1}{x}} \right| - 6 = 0\)

Tìm các giá trị của tham số m sao cho phương trình sau có nghiệm duy nhất : |mx – 2| = |x + 4| (*)

Với giá trị của a thì phương trình sau vô nghiệm ?

\(\frac{{x + 1}}{{x - a + 1}} = \frac{x}{{x + a + 2}}\)

Giải và biện luận hệ phương trình

a) \(\left\{ \begin{array}{l}
x - my = 0\\
mx - y = m + 1
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
2ax + 3y = 5\\
\left( {a + 1} \right)x + y = 0
\end{array} \right.\)

Giải hệ phương trình sau (có thể dùng máy tính bỏ túi để kiểm tra kết quả - Xem bài đọc thêm trang 94)

\(\left\{ \begin{array}{l}
x + y + z = 11\\
2x - y + z = 5\\
3x + 2y + z = 24
\end{array} \right.\)

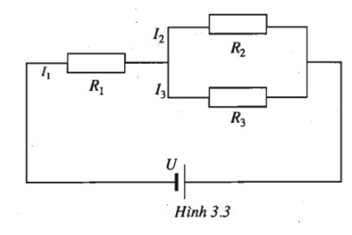
Cho một mạch điện kín. Biết R₁ = 0,250, R₂ = 0,360, R₃ = 0,450 và U = 0,6V. Gọi I₁ là cường độ dòng điện của mạch chính, I₂ và I₃ là cường độ dòng diện của mạch rẽ. Tính I₁, I₂, I₃ (chính xác đến phần trăm).

Cho một hệ hai phương trình bậc nhất hai ẩn. Biết rằng phương trình thứ hai trong hệ vô nghiệm. Hãy chọn kết luận đúng trong các khẳng định sau:

(A) Hệ đã cho nghiệm đúng với mọi giá trị của ẩn;

(B) Hệ đã cho vô nghiệm;

(C) Tập nghiệm của hệ đã cho trùng với tập nghiệm của phương trình thứ nhất;

(D) Không có kết luận gì.

Tính nghiệm gần đúng của hệ phương trình sau (chính xác đến hàng phần trăm):

a) \(\left\{ \begin{array}{l}
\sqrt 3 x - y = 1\\
5x + \sqrt 2 y = \sqrt 3 
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
4x + \left( {\sqrt 3  - 1} \right)y = 1\\
\left( {\sqrt 3  + 1} \right)x + 3y = 5
\end{array} \right.\)

Một miếng đất hình chữ nhật có chu vi 2p (mét). Nếu mở rộng miếng đất đó bằng cách tăng một cạnh thêm 3m và cạnh kia thêm 2m thì diện tích miếng đất tăng thêm 246 m². Tính các kích thước của miếng đất đó (biện luận theo p).

Giải và biện luận các hệ phương trình 

a) \(\left\{ \begin{array}{l}
x + my = 1\\
mx - 3my = 2m + 3
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
mx + y = 4 - m\\
2x + \left( {m - 1} \right)y = m
\end{array} \right.\)

Với giá trị nào của a thì mỗi hệ phương trình sau có nghiệm?

a) \(\left\{ \begin{array}{l}
\left( {a + 1} \right)x - y = a + 1\\
x + \left( {a - 1} \right)y = 2
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
\left( {a + 2} \right)x + 3y = 3a + 9\\
x + \left( {a + 4} \right)y = 2
\end{array} \right.\)

Tìm tất cả các cặp số nguyên (a, b) sao cho hệ phương trình sau vô nghiệm:

\(\left\{ \begin{array}{l}
ax + y = 2\\
6x + by = 4
\end{array} \right.\)

Cho hai đường thẳng (d₁): x + my = 3 và (d₂): mx + 4y = 6.

a) Với giá trị nào của m thì hai đường thẳng đó cắt nhau?

b) Với giá trị nào của m thì hai đường thẳng ấy song song với nhau?

c) Với giá trị nào của m thì hai đường thẳng ấy trùng nhau?

Giải hệ phương trình 

\(\left\{ \begin{array}{l}
x - y + z = 7\\
x + y - z = 1\\
 - x + y + z = 3
\end{array} \right.\)

Bài toán máy bơm nước.

Một gia đình muốn mua một chiếc máy bơm nước. Có hai loại có cùng lưu lượng nước bơm được trong một giờ: loại thứ nhất giá 1,5 triệu đồng, loại thứ hai giá 2 triệu đồng. Tuy nhiên, nếu dùng máy bơm loại thứ nhất thì mồi giờ tiền điện phải trả là 1200 đồng, trong khi dùng máy bơm loại thứ hai thì phải trả 1000 đồng, cho mỗi giờ bơm.

Kí hiệu f(x) và g(x) lần lượt là số tiền (tính bằng nghìn đồng) phải trả khi sử dụng máy bơm loại thứ nhất và loại thứ hai trong X giờ (bao gồm tiền điện và tiền mua máy bơm).

a) Hãy biểu diễn f(x) và g(x) dưới dạng các biểu thức của X.

b) Vẽ đồ thị của y = f(x) và y = g(x) trên cùng một mặt phẳng tọa độ.

c) Xác định tọa độ giao điểm của hai đồ thị ấy. Hãy phân tích ý nghĩa kinh tế của giao điểm đó.

Giải các hệ phương trình 

a) \(\left\{ \begin{array}{l}
x - y = 2\\
{x^2} + {y^2} = 164
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
{x^2} - 5xy + {y^2} = 7\\
2x + y = 1
\end{array} \right.\)

Giải các hệ phương trình

a) \(\left\{ \begin{array}{l}
{x^2} + {y^2} + x + y = 8\\
xy + x + y = 5
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
{x^2} + {y^2} - x + y = 2\\
xy + x - y =  - 1
\end{array} \right.\)

c) \(\left\{ \begin{array}{l}
{x^2} - 3x = 2y\\
{y^2} - 3y = 2x
\end{array} \right.\)

Tìm quan hệ giữa S và P để hệ phương trình sau có nghiệm:

\(\left\{ \begin{array}{l}
x + y = S\\
xy = P
\end{array} \right.\)

(S và P là hai số cho trước)

Giải các hệ phương trình sau:

a) \(\left\{ \begin{array}{l}
{x^2} + {y^2} = 208\\
xy = 96
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
{x^2} - {y^2} = 55\\
xy = 24
\end{array} \right.\)

Tìm hàm số bậc hai y = f(x) thỏa mãn các điều kiện sau :

a) Parabol y = f(x) cắt trục tung tại điểm (0; - 4)

b) f(2) = 6

c) Phương trình f(x) = 0 có hai nghiệm và hiệu giữa nghiệm lớn và nghiệm bé bằng 5

Phương trình ax + b = 0 có thể có nghiệm trong những trường hợp nào?

Giả sử ba phương trình f(x).g(x) = 0, f(x) = 0 và g(x) = 0 (với cùng tập xác định) có các tập nghiệm lần lượt là T, T₁ và T₂. Hãy chọn kết luận đúng trong hai kết luận sau:

a) S = S₁ ∩ S₂;

b) S = S₁ ∪ S₂.

Hệ phương trình dạng \(\left\{ \begin{array}{l}
ax + by = c\\
a'x + b'y = c'
\end{array} \right.\) (\({a^2} + {b^2} \ne 0\) và \(a{'^2} + b{'^2} \ne 0\)) có thể có nghiệm trong trường hợp nào ?

Áp dụng: Tìm a để hệ phương trình \(\left\{ \begin{array}{l}
ax + y = {a^2}\\
x + ay = 1
\end{array} \right.\) có nghiệm ?

Biết rằng phương trình ax² + bx + c = 0 có một nghiệm kép xo. Hãy chọn mệnh đề đúng trong các mệnh đề sau:

(A) Tam thức bậc hai ax² + bx + c có thể viết dưới dạng bình phương của một nhị thức bậc nhất;

(B) Parabol y = ax² + bx + c có đỉnh thuộc trục hoành;

(C) Phương trình cx² + bx + a = 0 cũng có một nghiệm kép là \(\frac{1}{{{x_0}}}\)

Giải và biện luận phương trình: m(mx –1) = x + 1

Cho phương trình p(x + 1) − 2x = p² + p − 4. Tìm các giá trị của p để:

a) Phương trình nhận 1 làm nghiệm;

b) Phương trình có nghiệm;

c) Phương trình vô nghiệm.

Ba cạnh của một tam giác vuông có độ dài là 3 số tự nhiên liên tiếp. Tính độ dài của chúng.

Cho phương trình (m − 1)x² + 2x − 1 = 0

a) Giải và biện luận phương trình.

b) Tìm các giá trị của m sao cho phương trình có hai nghiệm khác dấu.

c) Tìm các giá trị của m sao cho tổng bình phương hai nghiệm của nó bằng 1.

Với giá trị nào của a thì hai phương trình sau có nghiệm chung:

x² + x + a = 0 và x² + ax + 1 = 0

Cho các phương trình:

x² + 3x − m + 1 = 0  (1) và 

2x² − x + 1 − 2p = 0    (2)

a) Biện luận số nghiệm của mỗi phương trình bằng đồ thị.

b) Kiểm tra lại kết quả trên bằng phép tính.

Giải các hệ phương trình 

a) \(\left\{ \begin{array}{l}
{x^2} + {y^2} + xy = 7\\
{x^2} + {y^2} - xy = 3
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
2{\left( {x + y} \right)^2} - xy = 1\\
{x^2}y + x{y^2} = 0
\end{array} \right.\)

Giải và biện luận các hệ phương trình

a) \(\left\{ \begin{array}{l}
mx + 3y = m - 1\\
2x + \left( {m - 1} \right)y = 3
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
5x + \left( {a - 2} \right)y = a\\
\left( {a + 3} \right)x + \left( {a + 3} \right)y = 2a
\end{array} \right.\)

Giải và biện luận các hệ phương trình

a) \(\left\{ \begin{array}{l}
x + y = 4\\
xy = m
\end{array} \right.\)

b) \(\left\{ \begin{array}{l}
3x - 2y = 1\\
{x^2} + {y^2} = m
\end{array} \right.\)

Tìm a, b và c để Parabol y = ax² + bx + c (P) có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.

Cho tam giác ABC có BC = a; AC = b; AB = c.Ta lấy một điểm M trên cạnh BC. Qua M, ta kẻ các đường thẳng ME và MF thứ tự song song với các cạnh AC và AB (E ∈ AB, F ∈ AC). Hỏi phải lấy điểm M cách B bao nhiêu để tổng ME + MF = l (l là độ dài cho trước)? Biện luận theo l, a, b và c