Bài tập 63 trang 102 SGK Toán 10 NC

Bài tập 63 trang 102 SGK Toán 10 NC

Ta có I(1;- 4) là đỉnh của (P) nên:

\(\left\{ \begin{array}{l}
 - \frac{b}{{2a}} = 1\\
 - 4 = a + b + c
\end{array} \right.\)

\(M\left( {2; - 3} \right) \in \left( P \right) \)

\(\Rightarrow  - 3 = 4a + 2b + c\)

Ta có hệ phương trình:

\(\left\{ \begin{array}{l}
2a + b = 0\\
a + b + c =  - 4\\
4a + 2b + c =  - 3
\end{array} \right. \)

\(\Leftrightarrow \left\{ \begin{array}{l}
a = 1\\
b =  - 2\\
c =  - 3
\end{array} \right.\)

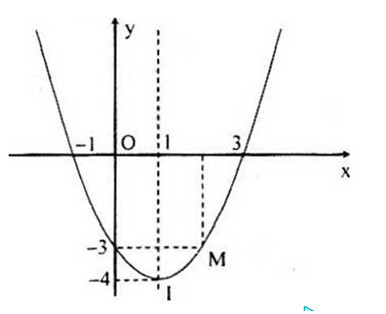
Vậy (P): y = x2 - 2x - 3

Đồ thị (P):

-- Mod Toán 10