Chương 2: Tích Vô Hướng Của Hai Vectơ Và Ứng Dụng

Chứng minh rằng trong tam giác ABC ta có:

a) \(sinA = sin(B + C)\)

b) \(cos A = -cos(B + C)\)

Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử \(\widehat{AOH}=\alpha\). Tính AK và OK theo a và \(\alpha\).

Chứng minh rằng :

a)  \(sin105^0 = sin75^0\);

b)  \(cos170^0 = -cos10^0\)

c)   \(cos122^0 = -cos58^0\)

Chứng minh rằng với mọi góc \(\alpha (0^0 \leq \alpha \leq 180^0)\) ta đều có \(cos^2 \alpha + sin^2 \alpha = 1\)

Cho góc x, với  \(cosx =\frac{1}{3}\)

Tính giá trị của biểu thức: \( P = 3sin^2x +cos^2x\)

Cho hình vuông ABCD,

Tính: \(cos(\overrightarrow{AC},\overrightarrow{BA}), sin(\overrightarrow{AC},\overrightarrow{BD}), cos(\overrightarrow{AB},\overrightarrow{CD})\) 

Cho tam giác vuông cân ABC có \(AB = AC = a\). Tính các tích vô hướng \(\overrightarrow{ AB} .\overrightarrow{AC };\overrightarrow{ AC} .\overrightarrow{CB }\).

Cho ba điểm O, A, B thẳng hàng biết \(OA = a, OB = b\). Tính tích vô hướng của \(\overrightarrow{OA}.\overrightarrow{OB}\) trong 2 trường hợp

a) Điểm O nằm ngoài đoạn AB

b) Điểm O nằm trong đoạn AB

Cho nửa đường tròn tâm O có  đường kính AB = 2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tai I.

a) Chứng minh  \(\overrightarrow{AI}.\overrightarrow{AM}= \overrightarrow{AI}.\overrightarrow{AB}\) và \(\overrightarrow{BI}.\overrightarrow{BN}= \overrightarrow{BI}.\overrightarrow{BA}\)

B) Hãy dùng câu a) để tính \(\overrightarrow{AI}.\overrightarrow{AM}+\overrightarrow{BI}.\overrightarrow{BN}\) theo R

Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4;2)

a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;

b) Tính chu vi tam giác OAB;

c) Chứng tỏ rằng OA vuông góc với AB và từ đó tính diện tích tam giác OAB

Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ  và  trong các trường hợp sau :

a) \(\vec{a}= (2; -3)\) , \(\vec{b}= (6; 4)\)

b)  \(\vec{a} = (3; 2)\), \(\vec{b}= (5; -1)\)

c)  \(\vec{a} = (-2; -2 \sqrt3)\), \(\vec{b}= (3; \sqrt3)\)

Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3); B(8; 4); C(1; 5); D(0;-2). Chứng minh rằng tứ giác ABCD là hình vuông.

Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đói xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ băng 2 sao cho tam giác ABC vuông ở C.

Cho tam giác ABC vuông tại A, \(\widehat{B} = 58^0\) và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh b, cạnh c và đường cao \(h_a\)_.

Cho tam giác ABC biết các cạnh a = 52, 1cm; b = 85cm và c = 54cm. Tính các góc \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\).

Cho tam giác ABC có \(\widehat{A}= 120^0\) cạnh b = 8cm và c = 5cm. Tính cạnh a, và góc \(\widehat{B}\), \(\widehat{C}\) của tam giác đó.

Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.

Tam giác ABC có \(\widehat{A} = 120^0\). Tính cạnh BC cho biết cạnh AC = m và AB = n.

Tam giác ABC có các cạnh a = 8cm, b = 10cm, c = 13cm

a) Tam giác đó có góc tù không? 

b) Tính độ dài đường trung tuyến MA của tam giác ABC đó.

Tính góc lớn nhất của tam giác ABC biết:

a) Các cạnh a = 3cm, b = 4cm, c = 6cm

b) Các cạnh a = 40cm, b = 13cm, c = 37cm

Cho tam giác ABC biết cạnh \(a = 137,5cm\); \(\widehat{B}= 83^0\) ; \(\widehat{C} = 57^0\). Tính góc A, cạnh b và c của tam giác.

Cho hình bình hành ABCD có AB = a, BC = b ,BD = m, và AC = n. Chứng minh rằng: \(m^2 + n^2 = 2(a^2 + b^2 )\)

Hai chiếc tàu thủy P và Q cách nhau 300m.TỪ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat{BPA}= 35^0, \widehat{BQA}= 48^0\) 

Tính chiều cao của tháp.

Muốn đo chiều cao của tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của giác kế có chiều cao h = 1,3 m. Gọi D là đỉnh tháp và hai điểm A_1, B₁, cùng thẳng  hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được \(\widehat{DA_1C_1}=49^0,\widehat{DB_1C_1}=35^0\).

Tính chiều cao của  CD của tháp đó.

Hãy nhắc lại định nghĩa giá trị lượng giác của một  góc \(\alpha \) với \({0^0} \le \alpha  \le {180^0}\). Tại sao khi \(\alpha \) là một góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?

Tại sao hai góc bù nhau lại có sin bằng nhau và cosin đối nhau?

Nhắc lại định nghĩa tích vô hướng của hai vectơ \(\vec a\) và \(\vec b\). Tích vô hướng này với |\(\vec a\) | và |\(\vec b\)| không đổi đạt giá trị lớn nhất và nhỏ nhẩt khi nào?

Hãy nhắc lại định lí cosin trong tam giác. Từ các hệ thức này hãy tính \(\cos A,\cos B,\cos C\) theo các cạnh của tam giác.

Trong mặt phẳng \({\rm{Oxy}}\) cho vecto \(\vec a = ( - 3;1)\) và vecto \(\vec b = (2;2)\) . Hãy tính tích vô hướng \(\vec a.\vec b.\)

Từ hệ thức \({a^2} = {b^2} + {c^2} - 2bc.\cos A\) trong tam giác, hãy suy ra định lí Py-ta-go.

Chứng minh rằng với mọi tam giác ABC, ta có  \(a = 2R\sin A;b = 2R\sin B;c = 2R\sin C\), trong đó \(R\) là bán kính đường tròn ngoại tiếp tam giác ABC.

Cho tam giác ABC. Chứng minh rằng:

a) Góc A nhọn khi và chỉ khi \({a^2} < {b^2} + {c^2}\)

b) Góc A tù khi và chỉ khi \({a^2} > {b^2} + {c^2}\)

c) Góc \(A\) vuông khi và chỉ khi \({a^2} = {b^2} + {c^2}\)

Cho tam giác ABC có góc \(A = {60^0},BC = 6\). Tính bán kính đường tròn ngoại tiếp tam giác đó.

Cho tam giác ABC có \(a = 12,b = 16,c = 20\). Tính diện tích \(S\)  tam giác,  chiều cao \({h_a}\), các bán kính R, r của các đường tròn ngoại tiếp, nội  tiếp tam giác và đường trung tuyến \({m_a}\) của tam giác.

Trong tập hợp các tam giác có hai cạnh là a và b. Tìm tam giác có diện tích lớn nhất.

Trong các đẳng thức sau đây, đẳng thức nào đúng?

A. \(\sin {150^0} =  - \frac{{\sqrt 3 }}{2}\)

B. \(\cos {150^0} = \frac{{\sqrt 3 }}{2}\)

C. \(\tan {150^0} =  - \frac{1}{{\sqrt 3 }}\) 

D. \(\cot {150^0} = \sqrt 3 \)

Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?

\(\begin{array}{l}
A.\sin \alpha  = \sin \beta \\
B.\cos \alpha  =  - \cos \beta \\
C.\tan \alpha  =  - \tan \beta \\
D.\cot \alpha  = \cot \beta 
\end{array}\)

Cho \(\alpha \) là góc tù. Điều khẳng định nào sau đây là đúng?

A. \(\sin \alpha  < 0\)

B. \(\cos \alpha  > 0\)

C. \(\tan \alpha  < 0\)

D. \(\cot \alpha  > 0\)

Trong các khẳng định sau đây, khẳng định nào sai?

A. \(\cos {45^0} = \sin {45^0}\) 

B. \(\cos {45^0} = \sin {135^0}\)

C. \(\cos {30^0} = \sin {120^0}\)

D. \(\sin {60^0} = cos{120^0}\)

Hai góc nhọn \(\alpha \) và \(\beta \)  trong đó \(\alpha  < \beta \) . Khẳng định nào sau đây là sai?

A. \(\cos \alpha  = \cos \beta \)

B. \(\sin \alpha  < \sin \beta \)

C. \(\alpha  + \beta  = {90^0} \Rightarrow \cos \alpha  = \sin \beta \)

D. \(\tan \alpha  + \tan \beta  > 0\)

Tam giác ABC vuông ở \(A\) và có góc \(B = {30^0}\). Khẳng định nào sau đây là sai?

A. \({\rm{cosB}} = \frac{1}{{\sqrt 3 }}\) 

B. \(\sin C = \frac{{\sqrt 3 }}{2}\)

C. \(\cos C = \frac{1}{2}\)

D. \(\sin B = \frac{1}{2}\)

Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

A. \(\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}\) 

B. \(\cos \widehat {BAH} = \frac{1}{{\sqrt 3 }}\)

C. \(\sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}\)   

D. \(\sin \widehat {AHC} = \frac{1}{2}\)

Khẳng định nào sau đây là đúng?

A. \(\sin \alpha= \sin ({180^0}{\rm{ - }}\alpha )\)

B. \(\cos \alpha = \cos ({180^0}{\rm{ - }}\alpha )\)

C. \(\tan \alpha = \tan ({180^0}{\rm{ - }}\alpha )\)

D. \(\cot \alpha = \cot ({180^0}{\rm{ - }}\alpha )\)

Tìm khẳng định sai trong các khẳng định sau đây:

A. \(\cos {35^0} > \cos {10^0}\) 

B. \(\sin {60^0} < \sin {80^0}\)

C. \(\tan {45^0} < \tan {60^0}\) 

D. \(\cos {45^0} = \sin {45^0}\)

Tam giác ABC vuông ở \(A\) và có góc \(B = {50^0}\). Hệ thức nào sau đây là sai:

A. \((\overrightarrow {AB} ,\overrightarrow {BC} ) = {130^0}\) 

B. \((\overrightarrow {BC} ,\overrightarrow {AC} ) = {40^0}\)

C. \((\overrightarrow {AB} ,\overrightarrow {CB} ) = {50^0}\)

D. \((\overrightarrow {AC} ,\overrightarrow {CB} ) = {120^0}\)

Cho \(\vec a\) và \(\vec b\)là hai vecto cùng hướng và đều khác vecto \(\vec 0\) . Trong các kết quả sau đây, hãy chọn kết quả đúng.

A. \(\vec a.\vec b{\rm{  = }}|\vec a|.|\vec b|\) 

B.  \(\vec a.\vec b = 0\)

C. \(\vec a.\vec b =  - 1\)

D. \(\vec a.\vec b =  - |\vec a|.|\vec b|\)

Cho tam giác ABC vuông cân tại \(A\) có \(AB = AC = 30cm\). Hai đường trung tuyến BF và CE cắt nhau tại \(G\). Diện tích tam giác GFC là:

A. \(50c{m^2}\) 

B. \(50\sqrt 2 c{m^2}\)

C. \(75c{m^2}\)

D. \(15\sqrt {105} c{m^2}\)

Cho tam giác ABC vuông tại A có AB = 5cm, BC = 13cm.  Gọi góc \(\widehat {ABC} = \alpha \) và góc \(\widehat {ACB} = \beta \). Hãy chọn kết luận đúng khi so sánh α và β.

A. \(\beta  > \alpha \)

B. \(\beta  < \alpha \)

C. \(\beta  = \alpha \)

D. \(\alpha  \le \beta \)

Cho góc \(\widehat {xOy} = {30^0}\). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên Ox và Oy sao cho \(AB = 1\). Độ dài lớn nhất của đoạn OB bằng:

A. 1,5

B. \(\sqrt 3 \)

C. \(2\sqrt 2 \)

D. \(2\)

Cho tam giác ABC có \(BC = a,CA = b,AB = c\). Mệnh đề nào sau đây là đúng?

A. Nếu \({b^2} + {c^2} - {a^2} > 0\) thì góc \(A\) nhọn

B. Nếu \({b^2} + {c^2} - {a^2} > 0\) thì góc \(A\) tù

C. Nếu \({b^2} + {c^2} - {a^2} < 0\) thì góc \(A\) nhọn

D. Nếu \({b^2} + {c^2} - {a^2} > 0\) thì góc \(A\) vuông

Đường tròn tâm \(O\) bán kính \(R = 15cm\). Gọi \(P\) là một điểm cách tâm \(O\) một khoảng \(PO = 9cm\). Dây cung đi qua \(P\) và vuông góc với PO có độ dài là:

A. 22cm

B. 23cm

C. 24cm

D. 25cm

Cho tam giác ABC có \(AB = 8cm,AC = 18cm\) và có diện tích bằng \(64c{m^2}\). Giá trị \(\sin A\) là:

A. \(\frac{{\sqrt 3 }}{2}\) 

B. \(\frac{3}{8}\) 

C. \(\frac{4}{5}\) 

D. \(\frac{8}{9}\)

Cho hai góc nhọn \(a\) và β phụ nhau. Hệ thức nào sau đây là sai?

A.\(\sin a =  - \cos \beta \)

B. \(\cos a = \sin \beta\)

C. \(\tan a = \cot \beta\)

D. \(\cot a = \tan \beta\)

Bất đẳng thức nào dưới đây là đúng?

A. \(\sin {90^0} < \sin {150^0}\) 

B. \(\sin {90^0}15' < \sin {90^0}30'\)

C. \(\cos {90^0}30' > \cos {100^0}\)

D. \(\cos {150^0} > \cos {120^0}\)

Cho tam giác ABC vuông tại \(A\). Khẳng định nào dưới đây là sai?

A. \(\overrightarrow {AB} .\overrightarrow {AC}  < \overrightarrow {BA} .\overrightarrow {BC} \) 

B. \(\overrightarrow {AC} .\overrightarrow {CB}  < \overrightarrow {AC} .\overrightarrow {BC} \)

C. \(\overrightarrow {AB} .\overrightarrow {BC}  < \overrightarrow {CA} .\overrightarrow {CB} \)

D. \(\overrightarrow {AC} .\overrightarrow {BC}  < \overrightarrow {BC} .\overrightarrow {AB} \)

Tam giác ABC có \(AB = 4cm,BC = 7cm,CA = 9cm\). Giá trị của \(\cos A\) là:

A. \(\frac{2}{3}\) 

B. \(\frac{1}{3}\)

C. \(\frac{-2}{3}\)  

D. \(\frac{1}{2}\)

Cho hai điểm \(A(1;2)\) và \(B(3;4)\). Giá trị của \({\overrightarrow {AB} ^2}\) là:

A. \(4\)

B. \(4\sqrt 2 \)

C . \(6\sqrt 2 \)

D. \(8\)

Cho hai vecto \(\vec a = (4;3)\) ; và \(\vec b = (1;7)\). Góc giữa hai vecto \(\vec a\) và \(\vec b\) là:

A. \({90^0}\)

B. \({60^0}\) 

C. \({45^0}\)

D. \({30^0}\)

Cho hai điểm \(M = (1; - 2)\) và \(N = ( - 3;4)\). Khoảng cách giữa hai điểm \(M\) và \(N\) là:

A. \(4\)  

B. \(6\)

C. \(3\sqrt 6 \)

D.  \(2\sqrt {13} \)

Tam giác ABC có \(A = ( - 1;1);B = (1;3)\) và \(C = (1; - 1)\). Trong các cách phát biểu sau đây, hãy chọn cách phát biểu đúng.

A. ABC là tam giác có ba cạnh bằng nhau

B. ABC là tam giác có ba góc đều nhọn

C. ABC là tam giác cân tại \(B\) (có \(BA = BC\))

D. ABC là tam giác vuông cân tại \(A\)

Tam giác ABC có \(A = (10;5),B = (3;2),C = (6; - 5)\). Khẳng định nào sau đây là đúng?

A. ABC là tam giác đều

B. ABC là tam giác vuông cân tại \(B\)

C. ABC là tam giác vuông cân tại \(A\)

D. ABC là tam giác có góc tù tại \(A\)

Tam giác ABC vuông cân tại \(A\) và nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Gọi \(r\) là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số \(\frac{R}{r}\) là:

A. \(1 + \sqrt 2 \)       

B. \(\frac{{2 + \sqrt 2 }}{2}\)

C. \(\frac{{\sqrt 2  - 1}}{2}\) 

D. \(\frac{{1 + \sqrt 2 }}{2}\)

Tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm. Khi đó đường trung tuyến AM của tam giác có độ dài là:

A. 8cm

B. 10cm

C. 9cm

D. 7,5cm

Tam giác ABC có \(BC = a,CA = b,AB = c\) và có diện tích \(S\). Nếu tăng cạnh BC lên \(2\) lần đồng thời tăng cạnh CA lên \(3\) lần và giữ nguyên độ lớn của góc \(C\) thì khi đó diện tích tam giác mới được tạo nên bằng:

A. 2S           

B. 3S

C. 4S

D. 6S

Cho tam giác DEF có \(DE = DF = 10cm\) và \(EF = 12cm\). Gọi \(I\) là trung điểm của cạnh EF. Đoạn thẳng DI có độ dài là:

A. 6,5 cm    

B. 7cm

C. 8cm  

D. 4cm

Tính giá trị đúng của các biểu thức sau (không dùng máy tính bỏ túi hoặc bảng số)

a) (2sin30⁰+cos135⁰−3tan150⁰)(cos180⁰−cot60⁰)

b) sin²90⁰+cos²120⁰+cos²0⁰−tan²60⁰+cot²135⁰

Đơn giản các biểu thức

a) sin100⁰+sin80⁰+cos16⁰+cos164⁰

b) 2sin(180⁰−α)cotα−cos(180⁰−α)tanαcot(180⁰−α) với 0⁰ < α < 90⁰.

Chứng minh các hệ thức sau:

a) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = )

b) \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha  \ne {{90}^0}} \)

c) \(1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }}\left( {{0^0} < \alpha  < {{180}^0}} \)

Trong các trường hợp nào tích vô hướng \(\overrightarrow a .\overrightarrow b \) có giá trị dương, có giá trị âm, bằng 0 ?

Cho tam giác ABC. Tổng 

\(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \left( {\overrightarrow {BC} ,\overrightarrow {CA} } \right) + \left( {\overrightarrow {CA} ,\overrightarrow {AB} } \right)\)

có thể nhận giá trị nào trong các giá trị sau: 90⁰; 180⁰; 270⁰; 360⁰ ?

Cho tam giác ABC vuông ở A và góc B = 30⁰. Tính giá trị của các biểu thức sau

a) \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \sin \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) + \tan \frac{{\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)}}{2}\)

b) \(\sin \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) + \cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) + \cos \left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right)\)

Cho bốn điểm bất kì A, B, C, D. Chứng minh rằng

\(\overrightarrow {DA} .\overrightarrow {BC}  + \overrightarrow {DB} .\overrightarrow {CA}  + \overrightarrow {DC} .\overrightarrow {AB}  =  0 \).

Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.

Chứng minh rằng điều kiện cần và đủ để tam giác ABC vuông tại A là \(\overrightarrow {BA} .\overrightarrow {BC}  = A{B^2}\)

Cho tam giác ABC với ba đường trung tuyến AD, BE, CF. Chứng minh rằng

\(\overrightarrow {BC} .\overrightarrow {AD}  + \overrightarrow {CA} .\overrightarrow {BE}  + \overrightarrow {AB} .\overrightarrow {CF}  = 0\).

Cho hai điểm M, N nằm trên đường tròn đường kính AB = 2R. Gọi I là giao điểm của hai đường thẳng AM, BN.

a) Chứng minh rằng \(\overrightarrow {AM} .\overrightarrow {AI}  = \overrightarrow {AB} .\overrightarrow {AI} ;\overrightarrow {BN} .\overrightarrow {BI}  = \overrightarrow {BA} .\overrightarrow {BI} \)

b) Tính \(\overrightarrow {AM} .\overrightarrow {AI}  + \overrightarrow {BN} .\overrightarrow {BI} \) theo R.

Cho hai đường thẳng a và b cắt nhau tại M. Trên a có hai điểm A và B, trên b có hai điểm C và D đều khác M sao cho \(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD} \). Chứng minh rằng bốn điểm A, B, C, D cùng nằm trên một đường tròn.

Cho đoạn thẳng AB cố định, AB = 2a và một số k². Tìm tập hợp các điểm M sao cho MA²−MB² = k²

Trong mặt phẳng tọa độ, cho \(\overrightarrow u  = \frac{1}{2}\overrightarrow i  - 5\overrightarrow j \) và \(\overrightarrow v  = k\overrightarrow i  - 4\overrightarrow j \).

a) Tìm các giá trị của k để \(\overrightarrow u  \bot \overrightarrow v \);

b) Tìm các giá trị của k để \(\left| {\overrightarrow u } \right| \bot \left| {\overrightarrow v } \right|\).

Trong mặt phẳng tọa độ, cho tam giác ABC có các đỉnh A(−4;1), B(2;4), C(2;−2).

a) Tính chu vi và diện tích của tam giác đó.

b) Tìm tọa độ của trọng tâm G, trực tâm H và tâm I của đường tròn ngoại tiếp tam giác ABC. Từ đó hãy kiểm tra tính chất thẳng hàng của ba điểm I, G, H.

Tam giác ABC có a = 12, b = 13, c = 15. Tính cosA và gócA.

Cho tam giác ABC có AB = 5, AC = 8, góc A = 60⁰. Kết quả nào trong các kết quả sau là độ dài cạnh BC?

a) \(\sqrt {129} \);                                            

b) 7;

c) 49;                                                  

d) \(\sqrt {69} \).

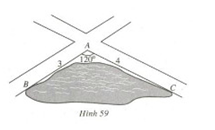
Hình 59 vẽ một hồ nước nằm ở góc tạo bởi hai con đường. Bốn bạn An, Cường , Trí, Đức dự đoán khoảng cách từ B đến C như sau

An :         5km

Cường :   6km

Trí :         7km

Đức :       5,5km

Biết rằng khoảng cách từ A đến B là 3km, khoảng cách từ A đến C là 4km, góc BAC là 120⁰.

Hỏi dự đoán của bạn nào sát với thực tế nhất ?

Cho tam giác ABC. Chứng minh các khẳng định sau

a) Góc A nhọn khi và chỉ khi a² < b²+c²;

a) Góc A tù khi và chỉ khi a² > b²+c²;

a) Góc A vuông khi và chỉ khi a² = b²+c².

Tam giác ABC có \(\widehat A = {60^0},\widehat B = {45^0},b = 4\).

Tính hai cạnh a và c.

Cho tam giác ABC có góc A = 60⁰, a = 6. Tính bán kính đường tròn ngoại tiếp tam giác.

Chứng minh rằng nếu ba góc của tam giác ABC thỏa mãn hệ thức sinA = 2sinB.cosC thì ABC là tam giác cân

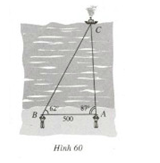
Hình 60 vẽ một chiếc tàu thủy đang neo đậu ở vị trí C trên biển và hai người ở các vị trí quan sát A và B cách nhau 500m. Họ đo được góc CAB bằng 87⁰ và góc CBA bằng 62⁰.

Tính các khoảng cách AC và BC.

Gọi H là trực tâm của tam giác không vuông ABC. Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ABC, HBC, HCA, HAB bằng nhau.

Tam giác ABC có a = 7,b = 8,c = 6. Tính m_a

Tam giác ABC có a = 5, b = 4, c = 3. Lấy điểm D đối xứng với B qua C. Tính độ dài AD.

Cho hình bình hành ABCD có AB = 4, BC = 5, BD = $7$. Tính AC.

Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương của hai đường chéo.

Chứng minh rằng tam giác ABC vuông ở A khi và chỉ khi 5m²a = m²b+m²c.

Tam giác ABC có b = 6,12; c = 5,35; A = 84⁰. Tính diện tích tam giác đó.

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh rằng AB²+BC²+CD²+DA² = AC²+BD²+4MN².

Gọi S là diện tích và R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh rằng S = 2R²sinAsinBsinC.

Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.

Giải tam giác ABC, biết

a) c = 14, A = 60⁰, B = 40⁰;                   

b) b = 4,5; A = 30⁰, C = 750;

c) c = 35, A = 40⁰, C = 120⁰;  

d) a = 137,5; B = 83⁰, C=57⁰.

Giải tam giác ABC, biết

a) a = 6,3, b = 6,3, C = 54⁰;

b) b = 32, c = 45, A = 87⁰;

c) a = 7, b = 23, C = 130⁰.

Giải tam giác ABC, biết

a) a = 14, b = 18, c = 20; 

b) a = 6, b = 7,3, c = 4,8;

c) a = 4, b = 5, c = 7

Biết hai lực cùng tác dụng vào một vật và tạo với nhau góc 40⁰. Cường độ của hai lực đó là 3N và 4N. Tính cường độ của lực tổng hợp.

Từ vị trí A người ta quan sát một cây cao (h.61)

Biết AH = 4m, HB = 20m, BAC = 45⁰. Tính chiều cao của cây.

Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang. Tính chiều cao của tòa nhà (h.62).

Chứng minh các công thức sau:

a) \(\overrightarrow a .\overrightarrow b  = \frac{1}{2}\left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)\)

b) \(\overrightarrow a .\overrightarrow b  = \frac{1}{4}\left( {{{\left| {\overrightarrow a  + \overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)\)

Gọi G là trọng tâm tam giác ABC.

a) Chứng minh rằng với mọi điểm M, ta luôn có

MA²+MB²+MC² = 3MG²+GA²+GB²+GC².

b) Tìm tập hợp các điểm M sao cho MA²+MB²+MC² = k², trong đó k là một số cho trước.

Cho hình bình hành ABCD. Tìm tập hợp các điểm MM sao cho MA²+MB²+MC²+MD² = k², trong đó k là một số cho trước.

Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'. Chứng minh rằng

a) AI⊥CC′, AJ⊥BB′;

b) BC′⊥B′C.

Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho AM = \(\frac{1}{4}\)AC.

a)Tính các cạnh của tam giác BMN.

b) Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó.

c) Gọi I là giao điểm của  BN và AC. Tính CI.

d) Tính bán kính đường tròn ngoại tiếp tam giác BDN.

Trong mặt phẳng tọa độ, cho \(\overrightarrow e  = \left( {4;1} \right)\) và \(\overrightarrow f  = \left( {1;4} \right)\)

a) Tìm góc giữa các vectơ \(\overrightarrow e\)$\stackrel{}{}$ và \(\overrightarrow f\).

b) Tìm m để vec tơ \(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f \) vuông góc với trục hoành.

c) Tìm n để vec tơ \(\overrightarrow b  = n\overrightarrow e  + \overrightarrow f \) tạo với vec tơ \(\overrightarrow i  + \overrightarrow j \) một góc 45⁰.

Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là b²+c² = 5a² 

Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.

Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S, chiều cao h_a, các bán kính R, r của đường tròn ngoại tiếp, nội tiếp tam giác đó.

Cho tam giác ABC. Chứng minh rằng

a) \(\cot A = \frac{{{b^2} + {c^2} - {a^2}}}{{4S}}\) (S là diện tích tam giác ABC);

b) \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}\)

Cho hai đường tròn (O;R) và (O′;R′) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó ( E, F là các tiếp điểm). Chứng minh rằng CE = CF.

Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.

a) Chứng minh rằng AB²+CD² không đổi.

b) Chứng minh rằng PA²+PB²+PC²+PD² không phụ thuộc vào vị trí của điểm P.

Giá trị \(\cos {45^0} + \sin {45^0}\) bằng bao nhiêu ?

(A) 1

(B) \(\sqrt 2 \)                           

(C) \(\sqrt 3 \)

(D) 0.

Trong các đẳng thức sau, đẳng thức nào đúng ?

(A) \(\sin ({180^0} - \alpha ) =  - \cos \alpha \)

(B) \(\sin ({180^0} - \alpha ) =  - \sin \alpha \)

(C) \(\sin ({180^0} - \alpha ) = \sin \alpha \)

(D) \(\sin ({180^0} - \alpha ) = \cos \alpha \)

Trong các đẳng thức sau, đẳng thức nào sai ?

(A) \(\sin {0^0} + \cos {0^0} = 0\)

(B) \(\sin {90^0} + \cos {90^0} = 1\)

(C) \(\sin {180^0} + \cos {180^0} =  - 1\)

(D) \(\sin {60^0} + \cos {60^0} = \frac{{\sqrt 3  + 1}}{2}\)

Trong các hệ thức sau, hệ thức nào không đúng ?

(A) \({(\sin \alpha  + \cos \alpha )^2} = 1 + 2\sin \alpha \cos \alpha \)

(B) \({(\sin \alpha  - \cos \alpha )^2} = 1 - 2\sin \alpha \cos \alpha \)

(C) \({\cos ^4}\alpha  - {\sin ^4}\alpha  = {\cos ^2}\alpha  - {\sin ^2}\alpha \)

(D) \({\cos ^4}\alpha  + {\sin ^4}\alpha  = 1\)

Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 120⁰?

(A) \((\overrightarrow {MN} ,\overrightarrow {NP} )\)

(B) \((\overrightarrow {MO} ,\overrightarrow {ON} )\)

(C) \((\overrightarrow {MN} ,\overrightarrow {OP} )\)

(D) \((\overrightarrow {MN} ,\overrightarrow {MP} )\)

Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai ?

(A) \(\overrightarrow {MN} (\overrightarrow {NP}  + \overrightarrow {PQ} ) = \overrightarrow {MN} .\overrightarrow {NP}  + \overrightarrow {MN} .\overrightarrow {PQ} \)

(B) \(\overrightarrow {MP} .\overrightarrow {MN}  =  - \overrightarrow {MN} .\overrightarrow {MP} \)

(C) \(\overrightarrow {MN} .\overrightarrow {PQ}  = \overrightarrow {PQ} .\overrightarrow {MN} \)

(D) \((\overrightarrow {MN}  - \overrightarrow {PQ} ).(\overrightarrow {MN}  + \overrightarrow {PQ} ) = M{N^2} - P{Q^2}\)

Trong các hệ thức sau, hệ thức nào đúng ?

(A) \(|\vec a.\vec b| = |\vec a|.|\vec b|\)

(B) \(\sqrt {{{\vec a}^2}}  = |\vec a|\)

(C) \(\sqrt {{{\vec a}^2}}  = \vec a\)

(D) \(\vec a =  \pm |\vec a|\)

Trong mặt phẳng tọa độ, cho \(\vec a = (3;4),\vec b = (4; - 3)\). Kết luận nào sau đây là sai ?

(A) \(\vec a.\vec b = 0\)

(B) \(\vec a \bot \vec b\)

(C) \(|\vec a.\vec b| = 0\)

(D) \(|\vec a|.|\vec b| = 0\)

Trong mặt phẳng tọa độ, cho \(\vec a = (9;3)\). Vectơ nào sau đây không vuông góc với vectơ \(\vec a\)$\stackrel{}{}$?

(A) \(\vec v = (1; - 3)\)

(B) \(\vec v = (2; - 6)\)

(C) \(\vec v = (1;3)\)

(D) \(\vec v = ( - 1;3)\)

Tam giác ABC có a = 14, b = 18, c = 20. Kết quả nào sau đây là gần đúng nhất ?

(A) \(\hat B \approx {42^0}{50^\prime }\)

(B) \(\hat B \approx {60^0}{56^\prime }\)

(C) \(\hat B \approx {119^0}{04^\prime }\)

(D) \(\hat B \approx {90^0}\)

Nếu tam giác MNP có \(MP = 5,PN = 8,\widehat {MPN} = {120^0}\) thì độ dài cạnh MN ( làm tròn đến chữ số thập phân thứ nhất ) là

(A) 11,4

(B) 12,4

(C) 7,0$\mathrm{}$

(D) 12,0

Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau.

Đặt MP = q, PQ = m, PE = x, PF = y (h.64).

Trong các hệ thức sau, hệ thức nào đúng ?

(A) ME = EF = FQ

(B) \(M{E^2} = {q^2} + {x^2} - xq\)

(C) \(M{F^2} = {q^2} + {y^2} - yq\)

(D) \(M{Q^2} = {q^2} + {m^2} - 2qm\)

Tam giác ABC có BC = 10, \(\widehat A = {30^0}\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?

(A) 5

(B) 10

(C) \(\frac{{10}}{{\sqrt 3 }}\)

(D) \(10\sqrt 3 \)

Tam giác với ba cạnh là 5, 12 và 13 có diện tích bằng bao nhiêu ?                       

 (A) 30

(B) \(20\sqrt 2 \)

(C) \(10\sqrt 3 \)

(D) 20

Tam giác ABC có ba cạnh là 6, 10, 8. Bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ?

(A) \(\sqrt 3 \)

(B) 4

(C) 2

(D) 1

Tam giác ABC có \(\hat B = {60^0},\hat C = {45^0},AB = 5\). Hỏi cạnh AC bằng bao nhiêu ?

(A) \(5\sqrt 3 \)

(B) \(5\sqrt 2 \)

(C) \(\frac{{5\sqrt 6 }}{2}\)

(D) 10.