Bài tập 23 trang 65 SGK Hình học 10 NC

Bài tập 23 trang 65 SGK Hình học 10 NC

Trường hợp 1: Tam giác ABC có ba góc nhọn.

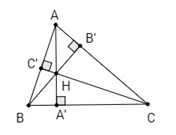
Gọi R, R₁ lần lượt là bán kính đường tròn ngoại tiếp tam giác ABC, HBC.

Áp dụng định lí sin ta có

\(\frac{{BC}}{{\sin A}} = 2R;\frac{{BC}}{{\sin \widehat {BHC}}} = 2{R_1}\)

Mà \(\widehat {BHC} + \widehat A = \widehat {B'HC'} + \widehat A = {180^0}\) 

(Vì 2 góc BHC và B′HC′ đối đỉnh)

⇒ sinA = sinBHC

Do đó  2R = 2R1 ⇒ R = R₁.

Vậy bán kính đường tròn ngoại tiếp tam giác HBC bằng bán kính đường tròn ngoại tiếp tam giác ABC.

Tương tự bán kính đường tròn ngoại tiếp tam giác HCA, HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.

Trường hợp 2: Tam giác ABC có góc tù.

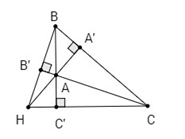
Ta có \(\frac{{BC}}{{\sin \widehat {BAC}}} = 2R;\frac{{BC}}{{\sin \widehat {BHC}}} = 2{R_1}\)

Mà \(\widehat {B'AC'} + \widehat {CHB} = {180^0}\sin \widehat {BAC} = \sin \widehat {B'AC'} = \sin \widehat {CHB}\)

(Vì BAC và B′AC′ đối đỉnh)

⇒ R = R₁ 

Tương tự ta chứng minh được bán kính đường tròn ngoại tiếp tam giác HCA, HAB bằng bán kính đường tròn ngoại tiếp tam giác ABC.

-- Mod Toán 10