Trang chủ
Lớp 10
Toán Lớp 10 SGK Cũ
Chương 2: Tích Vô Hướng Của Hai Vectơ Và Ứng Dụng
Bài tập 12 trang 73 SGK Hình học 10 NC
Bài tập 12 trang 73 SGK Hình học 10 NC
Lý thuyết
Bài tập
Câu hỏi:
Bài tập 12 trang 73 SGK Hình học 10 NC
Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau.
Đặt MP = q, PQ = m, PE = x, PF = y (h.64).
Trong các hệ thức sau, hệ thức nào đúng ?
(A) ME = EF = FQ
(B) \(M{E^2} = {q^2} + {x^2} - xq\)
(C) \(M{F^2} = {q^2} + {y^2} - yq\)
(D) \(M{Q^2} = {q^2} + {m^2} - 2qm\)
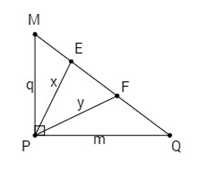
Ta có
\(\begin{array}{l}
M{F^2} = M{P^2} + F{P^2} - 2.MP.FP.\cos \widehat {MPF}\\
= {q^2} + {y^2} - 2.q.y\cos {60^0} = {q^2} + {y^2} - qy
\end{array}\)
Chọn (C).
-- Mod Toán 10
Copyright © 2021 HOCTAP247
