Bài tập 9 trang 52 SGK Hình học 10 NC
Bài tập 9 trang 52 SGK Hình học 10 NC
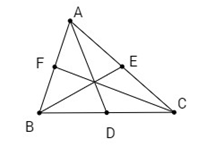
Cho tam giác ABC với ba đường trung tuyến AD, BE, CF. Chứng minh rằng
\(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} = 0\).
Ta có:
\(\begin{array}{l}
\overrightarrow {AD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\
\overrightarrow {BE} = \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\\
\overrightarrow {CF} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)
\end{array}\)
Do đó
\(\begin{array}{*{20}{l}}
{\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} }\\
\begin{array}{l}
= \frac{1}{2}\overrightarrow {BC} \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\overrightarrow {CA} \left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\\
+ \frac{1}{2}\overrightarrow {AB} \left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)
\end{array}\\
{ = \frac{1}{2}\left( \begin{array}{l}
\overrightarrow {BC} .\overrightarrow {AB} + \overrightarrow {BC} .\overrightarrow {AC} + \overrightarrow {CA} .\overrightarrow {BA} \\
+ \overrightarrow {CA} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CA} + \overrightarrow {AB} .\overrightarrow {CB}
\end{array} \right)}\\
\begin{array}{l}
= \frac{1}{2}\left( {\overrightarrow {BC} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {CB} } \right) + \frac{1}{2}\left( {\overrightarrow {BC} .\overrightarrow {AC} + \overrightarrow {CA} .\overrightarrow {BC} } \right)\\
+ \frac{1}{2}\left( {\overrightarrow {CA} .\overrightarrow {BA} + \overrightarrow {AB} .\overrightarrow {CA} } \right) = 0
\end{array}
\end{array}\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
