Bài tập 7 trang 52 SGK Hình học 10 NC
Bài tập 7 trang 52 SGK Hình học 10 NC
Cho bốn điểm bất kì A, B, C, D. Chứng minh rằng
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0 \).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.
Ta có:
\(\begin{array}{*{20}{l}}
{\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} }\\
\begin{array}{l}
= \overrightarrow {DA} \left( {\overrightarrow {DC} - \overrightarrow {DB} } \right) + \overrightarrow {DB} \left( {\overrightarrow {DA} - \overrightarrow {DC} } \right)\\
+ \overrightarrow {DC} \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)
\end{array}\\
\begin{array}{l}
= \overrightarrow {DA} .\overrightarrow {DC} - \overrightarrow {DA} .\overrightarrow {DB} + \overrightarrow {DB} .\overrightarrow {DA} \\
- \overrightarrow {DB} .\overrightarrow {DC} + \overrightarrow {DC} .\overrightarrow {DB} - \overrightarrow {DC} .\overrightarrow {DA} = 0
\end{array}
\end{array}\)
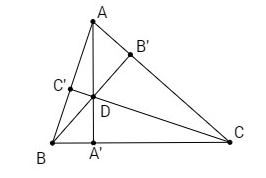
Gọi D là giao điểm của hai đường cao AA′, BB' của tam giác ABC.
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Từ đó suy ra \(\overrightarrow {DA} .\overrightarrow {BC} = 0,\overrightarrow {DB} .\overrightarrow {CA} = 0\), do đó DC ⊥ AB.
Vậy D nằm trên đường cao CC′ của tam giác ABC, tức là ba đường cao trong tam giác đồng quy.
-- Mod Toán 10
Copyright © 2021 HOCTAP247
