Bài tập 6 trang 51 SGK Hình học 10 NC
Bài tập 6 trang 51 SGK Hình học 10 NC
Cho tam giác ABC vuông ở A và góc B = 300. Tính giá trị của các biểu thức sau
a) \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \sin \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) + \tan \frac{{\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)}}{2}\)
b) \(\sin \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) + \cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) + \cos \left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right)\)
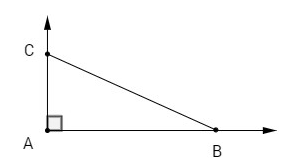
a) Ta có
\(\begin{array}{l}
\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {150^0};\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = {30^0};\\
\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {120^0}
\end{array}\)
Suy ra
\(\begin{array}{*{20}{l}}
{\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) + \sin \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) + \tan \frac{{\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)}}{2}}\\
\begin{array}{l}
= \cos {150^0} + \sin {30^0} + \tan {60^0}\\
= - \frac{{\sqrt 3 }}{2} + \frac{1}{2} + \sqrt 3 = \frac{{\sqrt 3 + 1}}{2}
\end{array}
\end{array}\)
b) Ta có \(\left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right) = {90^0}\), do đó:
\(\begin{array}{*{20}{l}}
{\sin \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) + \cos \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) + \cos \left( {\overrightarrow {CA} ,\overrightarrow {BA} } \right)}\\
\begin{array}{l}
= \sin {90^0} + \cos {30^0} + \cos {90^0}\\
= 1 + \frac{{\sqrt 3 }}{2} + 0 = \frac{{2 + \sqrt 3 }}{2}
\end{array}
\end{array}\)
-- Mod Toán 10
Copyright © 2021 HOCTAP247
